Post

05-动态规划

Posted Updated
By hhhi21g
8 min read

核心思想：拆分子问题，记住过往，减少重复计算

例子：青蛙跳阶问题(参考力扣70)

一个青蛙一次可以跳上1级台阶，也可以跳上2级台阶。求该青蛙跳上10级台阶总共有多少种跳法？

  • 到10
    • 先到9，再跳1；
    • 先到8，再跳2；

以此类推：定义f(n) = 跳到第n级台阶的跳法

有：

f(10) = f(9) + f(8);

f(9) = f(8) + f(7);

…

f(3) = f(2) + f(1)

而f(2) = 2,f(1) = 1很容易得出。

f(n) = f(n - 1) + f(n - 2)

1
2
3
4
5
6
7
8
9

class Solution {  //直接递归出现超时
    public int climbStairs(int n) {
        if(n == 1)
            return 1;
        else if(n == 2)
            return 2;
        return climbStairs(n-1) + climbStairs(n - 2);
    }
}

！！递归树中，一个子问题的事件复杂度为O(1)，共有2的n次幂-1个节点，因此总时间复杂度为O(2的次幂)！！

带备忘录的递归解法（自顶向下）

子问题数=树结点数=n,时间复杂度为O(n)

1
2
3
4
5
6
7
8
9
10
11
12
13
14

class Solution {
    //使用HashMap充当备忘录
    Map<Integer,Integer> tempMap = new HashMap();
    public int climbStairs(int n) {
        if(n == 0) return 1;
        if(n <= 2) return n;
        if(tempMap.containsKey(n)){
            return tempMap.get(n);
        }else{
            tempMap.put(n,climbStairs(n-1)+climbStairs(n-2));
            return tempMap.get(n);
        }
    }
}
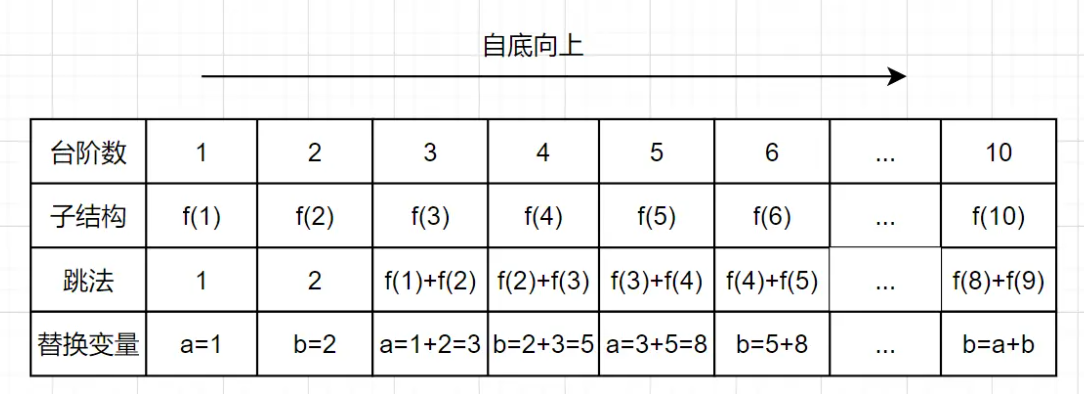
自底向上的动态规划

一些概念：以本题为例

  • f(n-1)和f(n-2)称为f(n)的最优子结构；
  • f(n) = f(n - 1) + f(n - 2)称为状态转移方程；
  • f(1) = 1,f(2) = 2为边界；
  • f(10) = f(9) + f(8),f(9) = f(8) + f(7)就是重叠子问题。

在本题中 ，f(n)只依赖与前面的两个数，因此只需要两个变量a和b存储；

alt text

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

class Solution {
    public int climbStairs(int n) {
        if(n <= 2)
            return n;
        int a = 1;
        int b = 2;
        int temp = 0;
        for(int i = 3;i<=n;i++){
            temp = a + b;
            a = b;
            b = temp;
        }
        return temp;
    }
}

最长公共子序列问题: 洛谷P1439

alt text

  • dp[i][j]:处理完第一个序列的前i个字符，第二个序列的前j个字符，现有的最长公共子序列；

  • dp[0][?],dp[?][0] = 0;

  • 状态转移方程：

    1
2

    dp[i][j] = dp[i-1][j-1] + 1, if a[i] = b[j]
           max{dp[i-1][j],dp[i][j-1]}, else

容易得到下面代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

package luogu;

import java.util.Scanner;

public class P1439 {

	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);
		int n = sc.nextInt();

		int[] a = new int[n + 1];
		int[] b = new int[n + 1];
		for (int i = 1; i <= n; i++) {
			a[i] = sc.nextInt();
		}
		for (int i = 1; i <= n; i++) {
			b[i] = sc.nextInt();
		}

		int[][] dp = new int[n + 1][n + 1];
		for (int i = 0; i <= n; i++) {
			for (int j = 0; j <= n; j++) {
				if (i == 0 || j == 0)
					dp[i][j] = 0;
				else if (a[i] == b[j])
					dp[i][j] = dp[i - 1][j - 1] + 1;
				else
					dp[i][j] = Math.max(dp[i][j - 1], dp[i - 1][j]);
			}
		}
		System.out.println(dp[n][n]);
	}
}

部分正确，但存在MLE,TLE

初步改进，使用滚动数组：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41

package luogu;

import java.util.Scanner;

public class P1439 {

	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);
		int n = sc.nextInt();

		int[] a = new int[n + 1];
		int[] b = new int[n + 1];
		for (int i = 1; i <= n; i++) {
			a[i] = sc.nextInt();
		}
		for (int i = 1; i <= n; i++) {
			b[i] = sc.nextInt();
		}

		// int[][] dp = new int[n + 1][n + 1];
		int[] cur = new int[n + 1];
		int[] pre = new int[n + 1];
		for (int i = 0; i <= n; i++) {
			for (int j = 0; j <= n; j++) {
				if (i == 0 || j == 0)
					cur[j] = pre[j] = 0;
				else if (a[i] == b[j])
					// dp[i][j] = dp[i - 1][j - 1] + 1;
					cur[j] = pre[j - 1] + 1;
				else
					// dp[i][j] = Math.max(dp[i][j - 1], dp[i - 1][j]);
					cur[j] = Math.max(cur[j - 1], pre[j]);
			}
			int[] temp = new int[n + 1];
			pre = cur;
			cur = temp;

		}
		System.out.println(pre[n]);
	}
}
  • 分析直接使用状态方程的代码可知，每一个dp的更新，只与本行和上一行的dp表有关；
  • 因此只需要存储当前行的cur[j],以及上一行的pre[j],代替二维数组即可；
  • 每一行更新完后，令pre = cur, cur置0，滚动起来。

滚动数组只减少了内存，在时间复杂度方面并没有改进，引出最终解法：LIS（最长上升子序列）

  • 原本先求两个序列的最长公共子序列，但b是a的一个重排；

    找LCS等价于找b在a中索引序列的LIS

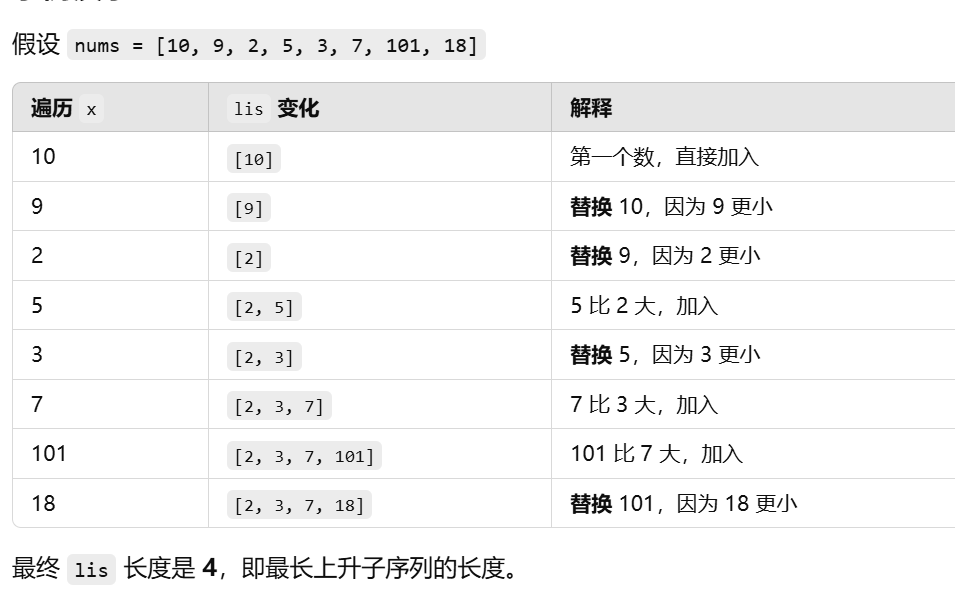
  • 使用贪心+二分查找：

    • 用数组lis存储当前构造的LIS；
    • 贪心策略：
      • 如果x比lis末尾大，x直接加入lis，即扩展lis;
      • 否则，用二分查找替换lis中第一个>=x的数，保证lis尽可能小，才能找到更长的上升序列；

alt text

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

package luogu;

import java.util.Arrays;
import java.util.HashMap;
import java.util.Map;
import java.util.Scanner;

public class P1439 {

	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);
		int n = sc.nextInt();

		Map<Integer,Integer> pos = new HashMap<>();
		
		// a[i]在原数组中的索引
		for(int i = 1;i<=n;i++) {
			int num = sc.nextInt();
			pos.put(num, i);
		}
		
		int[] indexSeq = new int[n];
		// 将b[i]映射至a的索引
		for(int i = 0;i<n;i++) {
			int num = sc.nextInt();
			indexSeq[i] = pos.get(num);
		}
		
		//indexSeq中为b在a中对应的索引序列
		int[] lis = new int[n];
		int length = 0;
		for(int x : indexSeq) {
			int posIdx = Arrays.binarySearch(lis, 0,length,x); //在lis数组中，从0到length寻找x
			if(posIdx<0) posIdx = -posIdx - 1;  //若没找到，计算插入下标
			lis[posIdx] = x; 
			if(posIdx == length) length++;  // 表示是当前lis中最大的数字，因此可以扩展序列
			//如果不是最大的，直接插入，挤掉了一个比x大的数，让lis变得更小
		}
		
		System.out.println(length);
	}
}
数据结构与算法
动态规划
This post is licensed under CC BY 4.0 by the author.