Post

04-图论

Posted Updated
By hhhi21g
9 min read
04-图论

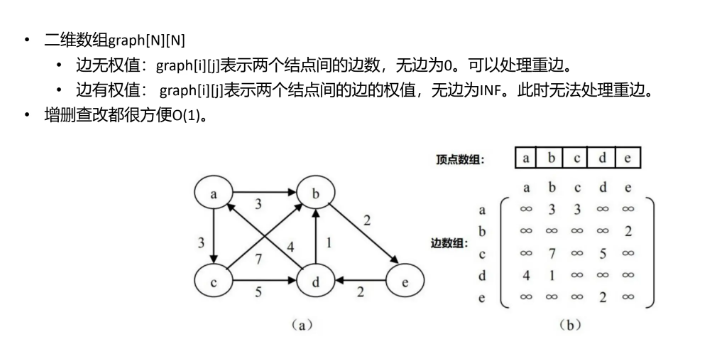
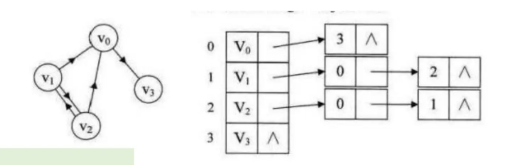
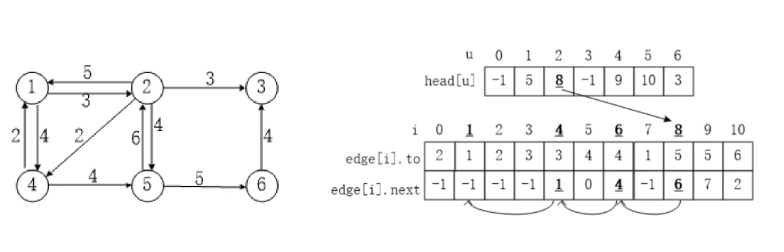
图的存储

  • 邻接矩阵

    alt text

  • 邻接表(最常用)

    alt text

  • 链式前向星(静态数组模拟临界表)

    alt text

  • 数组存边

图的遍历

不存在环，就不需要visited数组

例：力扣 797

alt text

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

class Solution {
    List<List<Integer>> res = new LinkedList<>();
    public List<List<Integer>> allPathsSourceTarget(int[][] graph) {
        LinkedList<Integer> path = new LinkedList<>();
        traverse(graph,0,path);
        return res;
    }
    
    void traverse(int[][] graph,int s,LinkedList<Integer> path){
        path.addLast(s);
        int n = graph.length;
        if(s == n-1){
            // 到达终点
            res.add(new LinkedList<>(path));  // 表示path的副本
            path.removeLast();
            return;
        }

        for(int v:graph[s])
            traverse(graph,v,path);

        path.removeLast();
    }
}

思路：

  • 从第一个节点开始试，先取一个它指向的节点，再依次取一个试下去；
  • 如果取到了终点，将这条路线的副本存到结果中，并把最后一个节点去掉；
  • 每一层试完，把最后一个节点去掉；

拓扑排序

  • 只有无环图才能进行拓扑排序；
  • 如果是有环图，可用于发现环的存在；

例：蓝桥 1337

alt text

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52

// BFS: 类似于人工方法
package lanQiao;

import java.util.ArrayList;
import java.util.LinkedList;
import java.util.List;
import java.util.Queue;
import java.util.Scanner;

public class L1337 {

	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);
		int n = sc.nextInt();
		int m = sc.nextInt();

		// 构建邻接表 & 统计入度
		List<Integer>[] graph = new ArrayList[n + 1];
		int[] inDegree = new int[n + 1];

		for (int i = 1; i <= n; i++)
			graph[i] = new ArrayList<>();

		for (int i = 0; i < m; i++) {
			int u = sc.nextInt();
			int v = sc.nextInt();
			graph[u].add(v);
			inDegree[v]++;
		}

		// 拓扑排序
		Queue<Integer> queue = new LinkedList<>();
		int[] dist = new int[n + 1];
		for (int i = 1; i <= n; i++) {
			if (inDegree[i] == 0)
				queue.add(i);
		}

        // 动态规划
		int maxDist = 0;
		while (!queue.isEmpty()) {
			int u = queue.poll();
			for (int v : graph[u]) {
				dist[v] = Math.max(dist[v], dist[u] + 1);
				maxDist = Math.max(maxDist, dist[v]);
				if (--inDegree[v] == 0)
					queue.add(v);
			}
		}
		System.out.print(maxDist);
	}
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54

// DFS
package lanQiao;

import java.util.ArrayList;
import java.util.List;
import java.util.Scanner;

public class L1337_bfs {
	static List<Integer>[] graph;
	static int[] memo; // 记忆化数组
	static boolean[] visited;

	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);
		int n = sc.nextInt();
		int m = sc.nextInt();

		graph = new ArrayList[n + 1];
		for (int i = 1; i <= n; i++) {
			graph[i] = new ArrayList<>();
		}

		for (int i = 0; i < m; i++) {
			int u = sc.nextInt();
			int v = sc.nextInt();
			graph[u].add(v);
		}

		memo = new int[n + 1];
		visited = new boolean[n + 1];

		int maxDist = 0;
		for (int i = 1; i <= n; i++) {
			maxDist = Math.max(maxDist, dfs(i));
		}
		System.out.print(maxDist);
	}

	// 递归计算从u开始的最长路径
	static int dfs(int u) {
		if (visited[u])
			return memo[u];
		visited[u] = true;

		int maxDepth = 0;
		for (int v : graph[u]) {
			maxDepth = Math.max(maxDepth, dfs(v) + 1);
		}

		memo[u] = maxDepth;
		return maxDepth;
	}
}

总结：

  • 邻接表的构建，与入度的计算；

  • 拓扑排序：以BFS为例

    • 使用queue存储当前入度为0的节点；

    • 动态规划思想：

      最初入度为0的节点，其最长路径一定为0；

      其下面一层的节点，有最长距离dist[v] = max{disk[v], disk[u]+1};

      若下面一层的节点入度值-1 == 0，说明到达该节点的最长路径值已经计算完毕，将其加入queue,继续进行计算

是否有环 & 环的输出

例：力扣 207——是否有环

alt text

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45

class Solution {
    boolean[] visit; // 有环图，判断是否访问过
    boolean[] onPath;  // 记录当前访问路径
    boolean hasCycle = false;
    
    public boolean canFinish(int numCourses, int[][] prerequisites) {
        List<Integer>[]graph = new ArrayList[numCourses];
        visit = new boolean[numCourses];
        onPath = new boolean[numCourses];

        for(int i = 0;i<numCourses;i++){
            graph[i] = new ArrayList<>();  
        }

        for(int[] edge: prerequisites){  // 建立邻接表
            graph[edge[1]].add(edge[0]);
        }

        for(int i = 0;i<numCourses;i++){
            traverse(graph,i);
            if(hasCycle) break;
        }

        return !hasCycle;
    }

    // DFS遍历
    void traverse(List<Integer>[] graph,int s){
        if(onPath[s]){
            // 当前遍历到的节点是当前遍历路径上的节点
            hasCycle = true;
        }

        if(visit[s] || hasCycle)
            return;
        
        visit[s] = true;
        onPath[s] = true;

        for(int v:graph[s]){
            traverse(graph,v);
        }
        onPath[s] = false;
    }
}

思路：

  • 顺着一条路一直走，如果走到了一个已经走过的节点，那么有环
  • 递归到一个节点的后续节点都试过，那么把这个点从尝试路径中去掉；
  • onPath: 当前路径

无向图的环检测：

同样用上面的方法，一般无向图在建图时需要记录两条边；

在进行无向图的环检测时，只进行一条边的统计。


例：洛谷 210——拓扑排序 & 有无环

alt text

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48

class Solution {
    boolean[] visit;
    boolean[] onPath;
    boolean hasCycle = false;
    List<Integer> order = new ArrayList<>();  // 存储后序遍历序列

    public int[] findOrder(int numCourses, int[][] prerequisites) {
        List<Integer>[] graph = new ArrayList[numCourses];
        visit = new boolean[numCourses];
        onPath = new boolean[numCourses];

        for(int i = 0;i<numCourses;i++){
            graph[i] = new ArrayList<>();
        }

        for(int []edge:prerequisites){
            graph[edge[1]].add(edge[0]);
        }

        for(int i = 0;i<numCourses;i++){
            traveres(graph,i);
            if(hasCycle) return new int[]{};
        }

        Collections.reverse(order);
        int[] res = new int[numCourses];
        for(int i = 0;i<numCourses;i++){
            res[i] = order.get(i);
        }
        return res;
    }

    void traveres(List<Integer>[] graph,int s){
        if(onPath[s]){
            hasCycle = true;
        }
        if(visit[s] || hasCycle)
            return;
        
        visit[s] = true;
        onPath[s] = true;
        for(int u:graph[s]){
            traveres(graph,u);
        }
        order.add(s);
        onPath[s] = false;
    }
}

思路：

  • 判断是否有环，同上一个例题相同；
  • 存储后序遍历序列
  • 将后序遍历序列反转，即为一条拓扑排序序列

注意：

  • ArrayList接口对应方法：

    add(i): 在尾部添加元素；

    get(i): 获得i位置的元素；

  • Collections.reverse() ：将列表内元素就地反转；


例：蓝桥 108——环的输出

alt text

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75

package lanQiao;

import java.util.ArrayList;
import java.util.HashSet;
import java.util.List;
import java.util.Scanner;
import java.util.Set;

public class L108 {

	static boolean[] visit;
	static boolean[] onPath;
	static boolean hasCycle = false;
	static Set<Integer> cycleNodes = new HashSet<>(); // 具有自动去重的功能
	static List<Integer> pathStack = new ArrayList<>();

	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);
		int n = sc.nextInt();
		visit = new boolean[n + 1];
		onPath = new boolean[n + 1];
		List<Integer>[] graph = new ArrayList[n + 1];
		for (int i = 0; i <= n; i++) {
			graph[i] = new ArrayList<>();
		}
		for (int i = 0; i < n; i++) { // 建立无向图的邻接表
			int u = sc.nextInt();
			int v = sc.nextInt();
			graph[u].add(v);
			graph[v].add(u);
		}
		traveres(graph, 1, -1);

		List<Integer> res = new ArrayList<>(cycleNodes);
		res.sort(Integer::compareTo);
		for (int i = 0; i < res.size(); i++) {
			if (i > 0)
				System.out.print(" ");
			System.out.print(res.get(i));
		}
		return;
	}

	static void traveres(List<Integer>[] graph, int s, int parent) {

		if (hasCycle)
			return;

		onPath[s] = true;
		pathStack.add(s);

		for (int v : graph[s]) {
			if (v == parent)
				continue; // 不回到父节点
			if (onPath[v]) {
				hasCycle = true;

				int idx = pathStack.lastIndexOf(v);
				for (int i = idx; i < pathStack.size(); i++) {
					cycleNodes.add(pathStack.get(i));
				}
				return;
			}
			if (!visit[v]) {
				visit[v] = true;
				traveres(graph, v, s);
				if (hasCycle)
					return;
			}
		}

		pathStack.remove(pathStack.size() - 1);
		onPath[s] = false;
	}
}
数据结构与算法
图论
This post is licensed under CC BY 4.0 by the author.