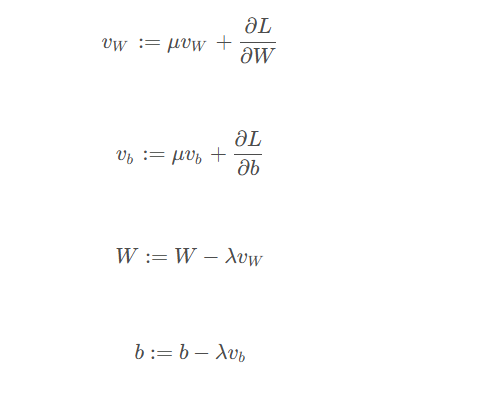强基1-优化函数

在深度学习中，优化器被用来调整模型的参数。优化器的目的是调整模型权重以最小化损失函数。

优化函数位于torch.optim包下

1.1 随机梯度下降算法——SGD

torch.optim.SGD(params, lr=, momentum=0, dampening=0, weight_decay=0, nesterov=False)

params (iterable) – 待优化参数的iterable或者是定义了参数组的dict \n lr (float) – 学习率 \n momentum (float, 可选) – 动量因子（默认：0）\n weight_decay (float, 可选) – 权重衰减（L2惩罚）（默认：0）\n dampening (float, 可选) – 动量的抑制因子（默认：0）\n nesterov (bool, 可选) – 使用Nesterov动量（默认：False）

SGD方程(无动量，左)(有动量，右)：

概念：振荡

在优化和梯度下降的背景下，”振荡“是指参数更新重复超过损失函数最小值的现象，导致参数的路径在损失曲面的斜率上来回振荡或曲折。更新不是平滑地收敛到最小值，而是不断地在其周围反弹，这可能会减慢收敛速度，使训练过程效率下降。(类比球的滚动，详见参考2)

没有动量的SGD

显示出蜿蜒曲折的模式，由于每一步仅基于局部梯度而采取，这可能导致过度校正，从而产生振荡。当损失表面具有陡峭的曲率时，这些调整是很大的，可能会导致更新超过最小值，从而导致在损失函数的斜坡上来回弹动。

有动量的SGD

动量的引入允许优化路径从先前步骤中累积方向性，这有助于平滑路径向最小值。动量项防止了优化器受到局部梯度变化的太大影响，从而导致较少的振荡和更直接的路径朝着目标前进。这通过更平滑和更稳定的曲线来展示，仍然朝着全局最小值前进，但途中的偏离较小。

动量有助于减弱振荡并提供更一致的行进方向，从而防止在没有动量的情况下看到的路径中出现的不稳定运动。这通常会导致更快的收敛速度和更有效的路径到达损失函数的最小值。

1.2 平均随机梯度下降算法——ASGD

1.3 Adagrad算法

1.4 自适应学习率调整——Adadelta算法

1.5 RMSprop算法

1.6 自适应矩估计——Adam算法

1.7 Adamax算法

1.8 SparseAdam算法

1.9 L-BFGS算法

1.10 弹性反向传播算法——Rprop算法

参考资料：

1. PyTorch学习之十种优化函数

2. 深度学习笔记:详解优化器之随机梯度下降（SGD）