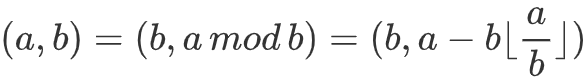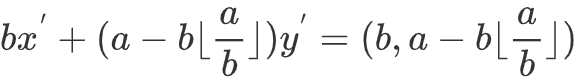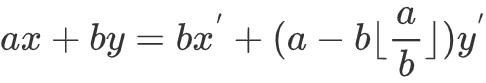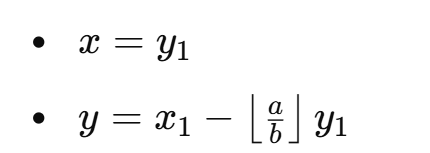03-数论
模运算
大数运算中的常用操作:如果一个数太大,无法直接输出,或者不需要直接输出,则可以对它取模,缩小数值再输出;
java中,如果存在负数,先按照正整数求余,然后再加上被除数的符号:
1 2 3 4
System.out.println(123 % 10); //3 System.out.println(123 % (-10)); //3 System.out.println((-123) % 10); //-3 System.out.println((-123) % (-10)); //-3
取模操作的性质:
加:(a+b) mod m =((a mod m)+(b modm)) mod m
减:(a-b) mod m =((a mod m) -(b mod m)) mod m
乘:(axb) mod m=((a mod m)×(b mod m)) mod m
除法不满足
快速幂、矩阵快速幂
快速幂
求 a n mod m,当n很大时;java直接用库函数modPow,变量用大数BigInteger
蓝桥1514
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
package lanQiao;
import java.math.BigInteger;
import java.util.Scanner;
public class L1514 {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
BigInteger base = sc.nextBigInteger(); // 底数
BigInteger exponent = sc.nextBigInteger(); // 幂
BigInteger modules = sc.nextBigInteger(); // 取模
BigInteger result = base.modPow(exponent, modules);
System.out.println(result);
}
}
蓝桥1157
这里使用小费马定理,只能在模为质数的时候使用;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
package lanQiao;
import java.math.BigInteger;
import java.util.Scanner;
public class L1157 {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int t = sc.nextInt();
BigInteger exponent = new BigInteger("1000000005");
BigInteger modules = new BigInteger("1000000007");
for (int i = 0; i < t; i++) {
BigInteger n = sc.nextBigInteger();
// modPow参数为两个BigInteger
BigInteger res = n.modPow(exponent, modules);
System.out.println(res);
}
}
}
蓝桥603
暴力计算p,q:从2到根号n,注意:BigInteger的用法
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24
public static void main(String[] args) { BigInteger n = new BigInteger("1001733993063167141"); BigInteger p = new BigInteger("2"); BigInteger i = BigInteger.valueOf(1); BigInteger j = BigInteger.valueOf(0); BigInteger q; for (; p.multiply(p).compareTo(n) != 1; p = p.add(i)) { if (n.mod(p) == j) { BigInteger sep = BigInteger.valueOf(2); for (; sep.multiply(sep).compareTo(p) != 1; sep = sep.add(i)) { if (p.mod(sep) == j) break; } if (sep.multiply(sep).compareTo(p) == 1) { break; } else { continue; } } } q = n.divide(p); System.out.println(p + " " + q); System.out.println(q.multiply(p)); } //891234941 1123984201
使用扩展欧几里得算法:
裴蜀定理:对于任意两个整数a、b,它们的最大公约数可以表示为a和b的线性组合,即存在整数x和y,使得ax + by = gcd(a,b);
本题中de % (p-1)(q -1) = 1,即有de = k(p-1)(q-1) + 1; ed - k(p-1)(q-1) = 1;
互质是逆元存在的充分必要条件
欧几里得算法,递归部分的核心如下:
扩展欧几里得算法: 根据裴蜀定理,带入欧几里得算法变式可得:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47
package lanQiao; import java.math.BigInteger; public class RSAjiemi { // 扩展欧几里得算法,计算 a 和 b 的最大公约数,同时返回线性组合的系数 x 和 y public static BigInteger[] extendedGCD(BigInteger a, BigInteger b) { // 基本情况,当 b 为 0 时,返回 a 和 (1, 0),即 ax + by = a if (b.equals(BigInteger.ZERO)) { return new BigInteger[] { a, BigInteger.ONE, BigInteger.ZERO }; } // 递归计算 BigInteger[] result = extendedGCD(b, a.mod(b)); BigInteger gcd = result[0]; BigInteger x1 = result[1]; BigInteger y1 = result[2]; // 计算 x 和 y BigInteger x = y1; BigInteger y = x1.subtract(a.divide(b).multiply(y1)); // gcb:a,b的最大公约数; x,y是等式ax + by = gcd(a,b)的解 return new BigInteger[] { gcd, x, y }; } public static void main(String[] args) { BigInteger p = new BigInteger("891234941"); BigInteger q = new BigInteger("1123984201"); BigInteger d = BigInteger.valueOf(212353); BigInteger n = new BigInteger("1001733993063167141"); BigInteger ps = p.subtract(BigInteger.ONE); BigInteger qs = q.subtract(BigInteger.ONE); BigInteger mul = ps.multiply(qs); //d与(p-1)*(q-1)互质 // 则result[1]是d在mod mul下的逆元 BigInteger[] result = extendedGCD(d, mul); BigInteger gcd = result[0]; BigInteger e = result[1]; BigInteger c = new BigInteger("20190324"); BigInteger res = c.modPow(e, n); System.out.println(res); } } // 579706994112328949
矩阵快速幂
[Fn, Fn-1, … ,Fn-k] = [Fn-1,Fn-2, … ,Fn-k-1]A = [Fk,Fk-1, … ,F0]An-k
蓝桥1180
很容易手算出A值,正常使用矩阵快速幂,注意:BigInteger类型创建数组不会自动初始化为0!!
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
package lanQiao;
import java.math.BigInteger;
import java.util.Scanner;
public class feibonaqie {
static final BigInteger MOD = new BigInteger("1000000007");
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int t = sc.nextInt();
BigInteger matrix[][] = { { BigInteger.ONE, BigInteger.ONE }, { BigInteger.ONE, BigInteger.ZERO } };
BigInteger res[][] = new BigInteger[2][2];
BigInteger fi;
for (int i = 0; i < t; i++) {
BigInteger n = sc.nextBigInteger();
BigInteger two = BigInteger.valueOf(2);
res = matrixPower(matrix, n.subtract(two));
fi = res[0][0].add(res[1][0]);
System.out.println(fi.mod(MOD));
}
}
public static BigInteger[][] matrixPower(BigInteger[][] matrix, BigInteger exp) {
int size = matrix.length;
BigInteger[][] res = new BigInteger[size][size];
BigInteger[][] base = matrix;
for (int i = 0; i < size; i++) {
for (int j = 0; j < size; j++) {
if (i == j)
res[i][j] = BigInteger.ONE;
else
res[i][j] = BigInteger.ZERO;
}
}
while (exp.compareTo(BigInteger.ZERO) == 1) {
if (exp.and(BigInteger.ONE).compareTo(BigInteger.ONE) == 0) {
res = multiplyMatrix(res, base);
}
base = multiplyMatrix(base, base);
BigInteger two = BigInteger.valueOf(2);
exp = exp.divide(two);
}
return res;
}
public static BigInteger[][] multiplyMatrix(BigInteger[][] a, BigInteger[][] b) {
int size = a.length;
BigInteger[][] res = new BigInteger[size][size];
for (int i = 0; i < size; i++) {
for (int j = 0; j < size; j++) {
res[i][j] = BigInteger.ZERO;
}
}
for (int i = 0; i < size; i++) {
for (int j = 0; j < size; j++) {
for (int k = 0; k < size; k++) {
BigInteger mid = a[i][k].multiply(b[k][j]);
res[i][j] = (res[i][j].add(mid)).mod(MOD);
}
}
}
return res;
}
}
用于图论最短路径问题
GCD和LCM
即最大公约数和最小公倍数
蓝桥210
模板题, 蓝桥杯规定的java版本为8,不支持Math.gcd()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
package lanQiao;
import java.util.Scanner;
public class hetaoCnt {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int a, b, c;
a = sc.nextInt();
b = sc.nextInt();
c = sc.nextInt();
int minCnt = lcm(lcm(a, b), c);
System.out.println(minCnt);
}
public static int gcd(int a, int b) {
if (b == 0) {
return a;
} else {
return gcd(b, a % b);
}
}
public static int lcm(int a, int b) {
if (a != 0 && b != 0) {
return a * b / gcd(a, b);
} else {
return 0;
}
}
}
蓝桥520
a * b /c 等同于 a / c * b,当数值较大时,先算乘法以防止溢出;
这里从根号b1的两边处理,减少扫描次数;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
package lanQiao;
import java.util.Scanner;
public class L520 {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
long a0, a1, b0, b1;
for (int i = 0; i < n; i++) {
a0 = sc.nextLong();
a1 = sc.nextLong();
b0 = sc.nextLong();
b1 = sc.nextLong();
int x;
int res = 0;
for (x = 1; x * x <= b1; x++) {
if (b1 % x == 0) {
if (gcd(x, a0) == a1 && lcm(x, b0) == b1)
res++;
if (x * x == b1)
break;
if (gcd(b1 / x, a0) == a1 && lcm(b1 / x, b0) == b1)
res++;
}
}
System.out.println(res);
}
}
public static long gcd(long a, long b) {
return b == 0 ? a : gcd(b, a % b);
}
public static long lcm(long a, long b) {
if (a != 0 && b != 0)
return a / gcd(a, b) * b; //防止中间结果溢出
else
return 0;
}
}
素数
很多定理,有空再说