算法与计算理论简单介绍
一、计算机物理模型的发展
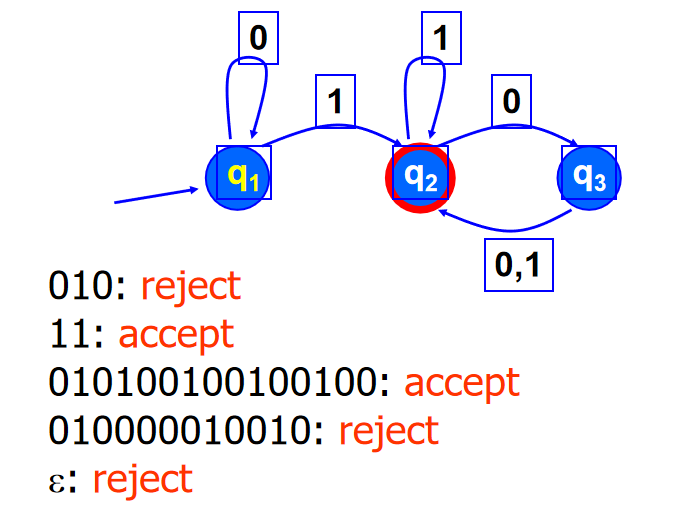
1. 接受状态:
在自动机中用一个特殊的状态来作回答,如果读完整个输入字符串后自动机停在这个特殊的状态,则算是Yes(接受),否则就是No(拒绝)。
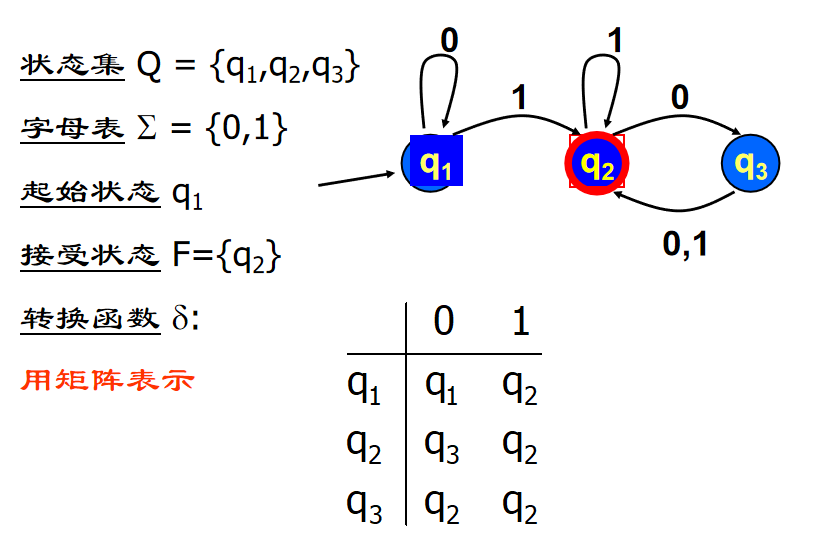
2. 确定性有限自动机(DFA)
使用五元组定义:M = (Q, Σ, δ, q0, F)
接受状态可以有多个
一个自动机M接受的所有字符串的集合用:L(M) 表示。L(M)是Σ上的一个语言,也称自动机M识别语言L(M)。
接受和识别本质上是同一个概念,接受的是字符串,识别的是语言,只是使用层级不同。
能被一台确定性有限自动机识别的语言称为正则语言。
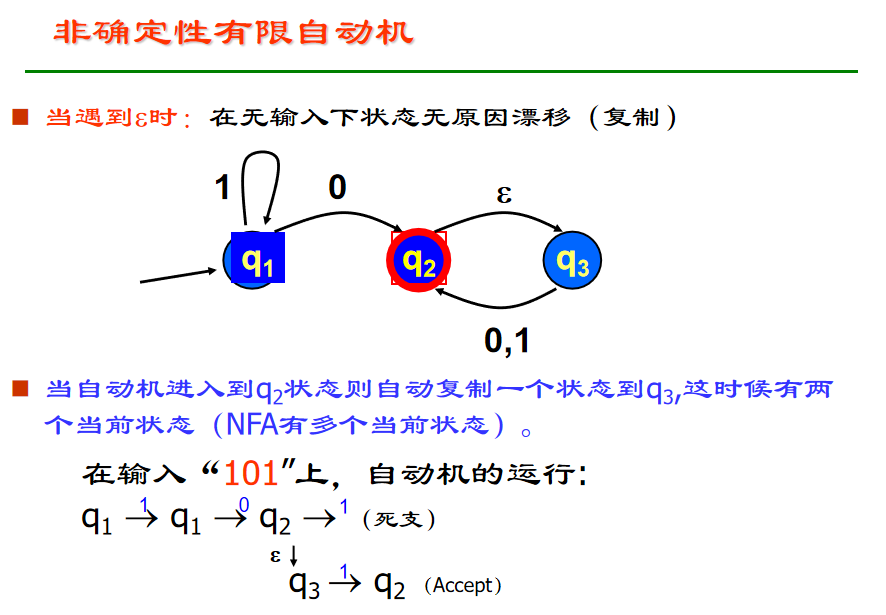
非确定性有限自动机:
状态转移时不确定转移到哪个状态,可以有多个选择,从而采用并行的方式,同时转移到所有需要转移的状态下。
确定性自动机给出的状态链是一条路径,而非确定性自动机给出的状态链是棵树。
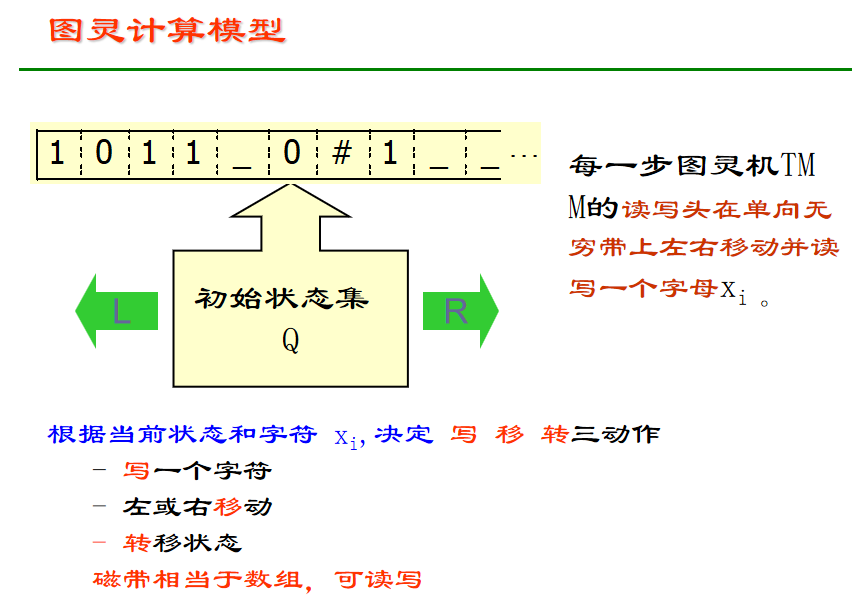
3. 图灵机
当前状态、当前带内容 和 读写头当前位置组合在一起
图灵机运行结果有三种可能:接受、拒绝、死循环
如果一个语言能被某一图灵机识别(语言中任何一个字符串作为输入,图灵机都接受),则称该语言是图灵可识别的,也称为递归可枚举语言;
拒绝的可能死循环
如果一个语言能被某一图灵机判定(图灵可识别,且任何一个字母表上的字符串作为输入,图灵机都停机),则称该语言是图灵可判定的,也称为递归语言。
二、计算问题的认识
1. 停机问题
| **停机问题:ATM = { <M,w> | M是TM且接受字符串w},证明停机问题是不可判定的。** |
假设存在一个万能的程序H,对于任意一个程序M和任意一个输入w,他能够给出M处理w的结果到底是接受还是拒绝的明确答复,并且永远不会死机;
以H为核心,构造出一个专门唱反调的程序D:
给D一个程序M,D先从H那里获得:“如果让M跑自己的代码,它是否会接受”;如果H回答接受,D就进入拒绝的状态;反之如果H不接受,D就进入接受的状态;
让D处理自己的代码D(对角线):
如果H回答,D会接受自己:D作出与H相反的答案,拒绝;
如果H回答,D拒绝自己:D接受;
H的回答无论如何都会错误。
只要H存在,就可以造出D;
一旦造出了D,H在D面前一定会出错;
但最初对H的定义是万能的;
最初的假设:存在万能判定器H,从逻辑上是不可能成立的!
如果停机问题是可判定的,那么ATM也就可判定的,停机了获得接受或拒绝的结果是简单的。从而就可以说,如果ATM不可判定的情况下,停机问题一定是不可判定的。
2. P类问题
P表示多项式时间
这类问题可以被计算机在很快的时间内解决。所谓快,是指随着问题规模n的增大,计算时间以n的常数次幂(如n2)增长。是计算机擅长解决的容易题。
P是确定型单带图灵机在多项式时间内可判定的语言类。
3. NP类问题
NP表示非确定性多项式时间
这类问题我们不确定能不能很快的找到答案,但如果给出一个潜在答案,计算机可以很快的验证这个答案对不对。
NP是具有多项式时间验证机的语言类。
- 一个语言在NP中,当且仅当它能被某个非确定型多项式时间图灵机判定。