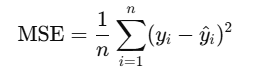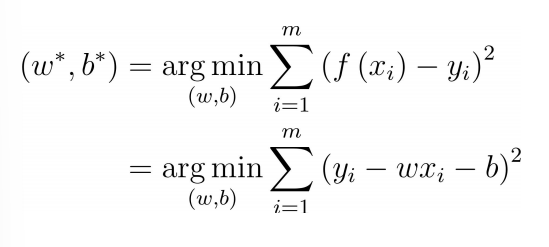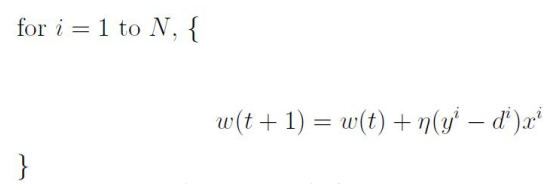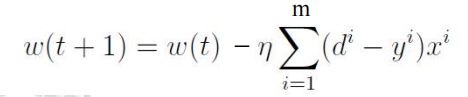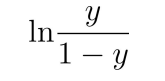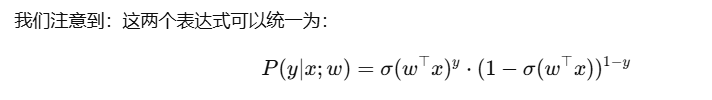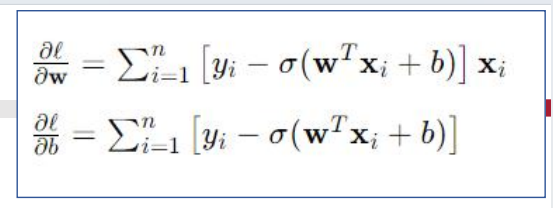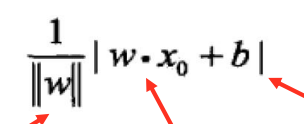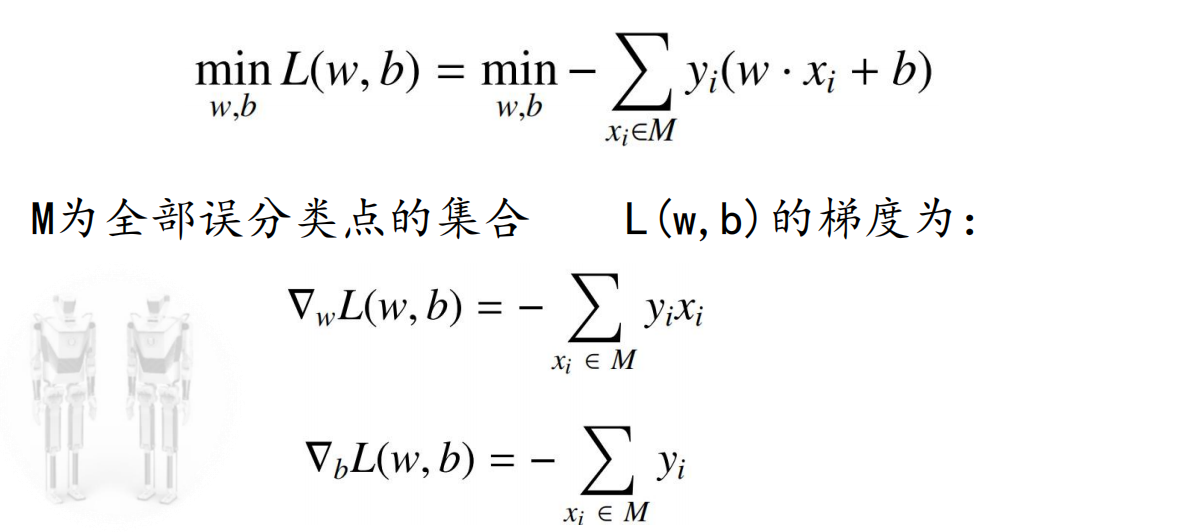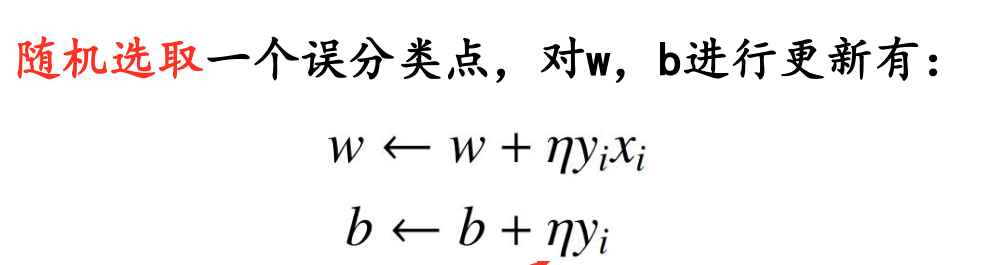机器学习第2讲——线性系统和感知机
线性模型
最小二乘法(least square method): 参数/模型估计
MSE(Mean Squared Error, 均方误差):有全局最优解和封闭解
使MSE最小:
先求出b, 求w时,将和展开,将b用求出的结果代替即可
最小二乘法的概率解释
P(y x; w) : 表示在给定输入特征x和模型参数w的条件下,输出y的概率或概率密度,即y落在某个值附近的可能性密度是多少。 - 极大似然法:寻找哪组参数最有可能产生当前观察到的数据
- 现在已知N个样本,L(w)为已知概率密度情况下,这N个样本同时出现的概率,取log;
- 既然这种情况已经发生,那么就需要找到参数w,使得L(w)最大,则w就是最可能的值。
梯度下降优化
随机梯度下降(stochastic gradient descent,SGD)
只选用随机选取的子集
批量梯度下降(batch gradient descent,BGD)
注:在较大的训练集的情况下,BGD算法计算量大;SGD算法在最小值的周边震荡,但可以较快收敛。
二分类任务
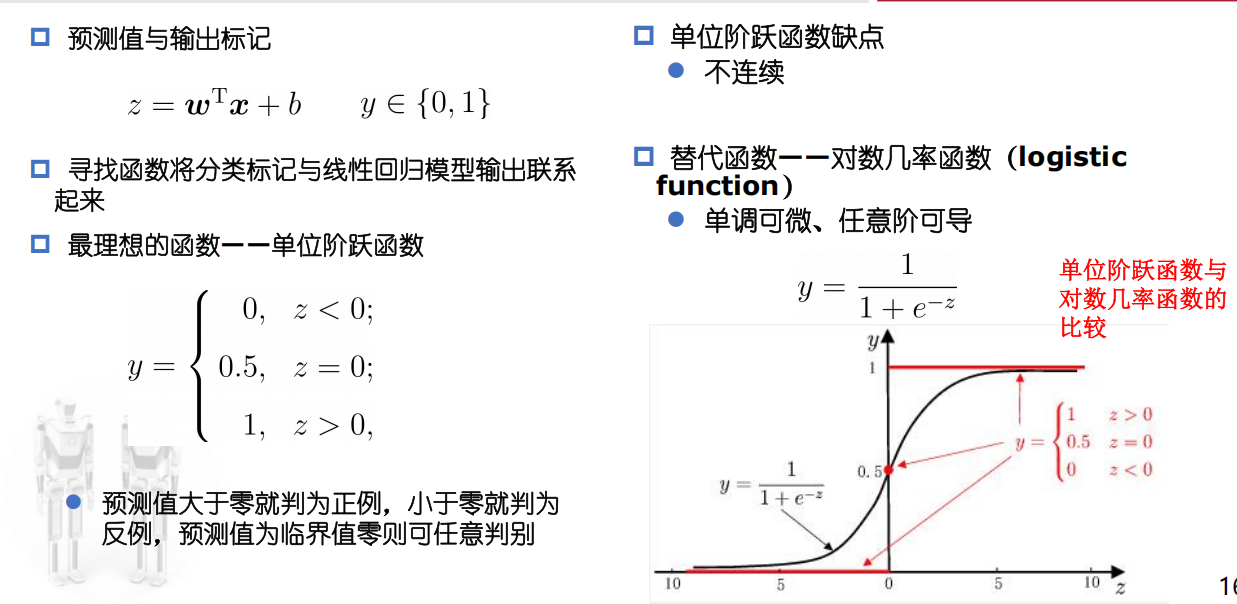
二分类任务——对数几率回归(Logistic回归)
核心思想:用一个线性函数来建模对数几率(log-odds),进而预测分类概率。
对数几率:
把概率p从(0,1)映射到实数范围,便于用线性模型建模。
对数几率回归的数学形式:
实例:
- 无需事先假设数据分布;
- 可得到“类别”的近似概率预测;
- 可直接应用现有数值优化算法求取最优解。
对数几率回归的极大似然法:
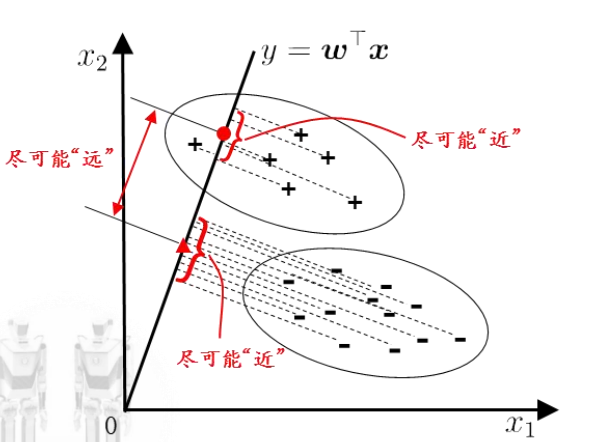
二分类任务——线性判别回归(Linear Discriminant Analysis,LDA)
给定训练集,设法将样例投影到一条直线上,使得同类样例的投影点尽可能接近、异类样例的投影点尽可能远离;
在对新样本进行分类时,将其投影到同样的这条直线上,再根据投影点的位置来确定新样本的类别。
也被视为一种监督降维技术
思想:
- 欲使同类样例的投影点尽可能接近,可以让同类样例投影点的协方差尽可能小;
- 欲使异类样例的投影点尽可能远离,可以让类中心之间的距离尽可能大。
感知机(perceptron)
二类分类的线性分类模型,输入为实例的特征向量,输出为实例的类别,取+1和-1二值。
定义:注意是点乘
几何意义
| 感知机模型的假设空间时定义在特征空间中的所有线性分类模型或线性分类器,**即函数集合{f | f(x) = w·x+b}** |
线性方程:w·x + b = 0 , 对应于特征空间中的一个超平面S
- w: 超平面的法向量
- b: 超平面的截距
超平面S将特征空间划分为两个部分,位于两部分的点分为正、负两类。因此,超平面S称为分离超平面(separating hyperplane)
数据集的线性可分性
如果存在一个超平面S,能够将数据集的正负样本点完全正确地划分到超平面的两侧,则称数据集为线性可分数据集;否则,则称数据集线性不可分。
感知机的学习策略
假设训练数据集是线性可分的;
感知机学习的目标是求得一个能够将训练集正实例点和负实例点完全正确分开的分离超平面;
为了找出这样的超平面,即确定感知机模型参数(w,b), 需要确定一个学习策略,即定义损失函数并将损失函数最小化;
损失函数:误分类点到超平面S的总距离
注:若使用误分类点的总数,这样的损失函数不是参数w,b的连续可导函数,不易优化;
输入空间内任一点x0到超平面S的距离:
普通的点到平面距离,向量版
由上得到感知机的损失函数:
为什么忽略了w的范数?\n
感知机的任务就是进行二分类工作,并不关心各点到超平面的距离。
优化方法
随机梯度下降SGD
算法流程:
例题(PPT16):
注:感知机模型和分离超平面不止一个
迭代收敛性
对于线性可分的数据集,感知机学习算法收敛:即经过有限次迭代可以得到一个将训练数据集样本完全正确划分的分离超平面。
若训练数据集线性不可分,感知机学习算法不收敛,迭代结果会反复振荡
感知机学习算法的对偶形式
一个问题的原始问题称为:primal problem;
对偶问题称为:dual problem
具体步骤:
例题(PPT31):