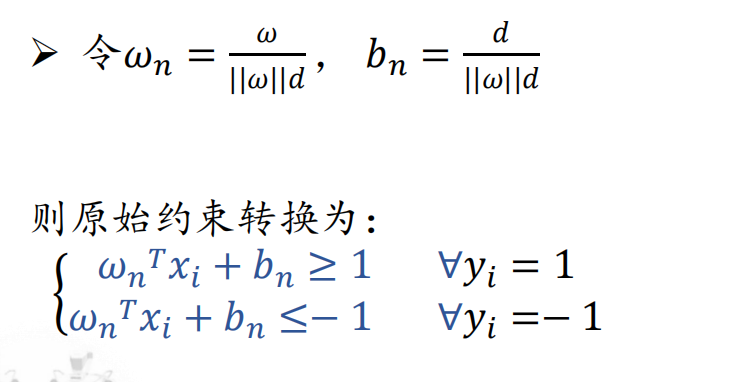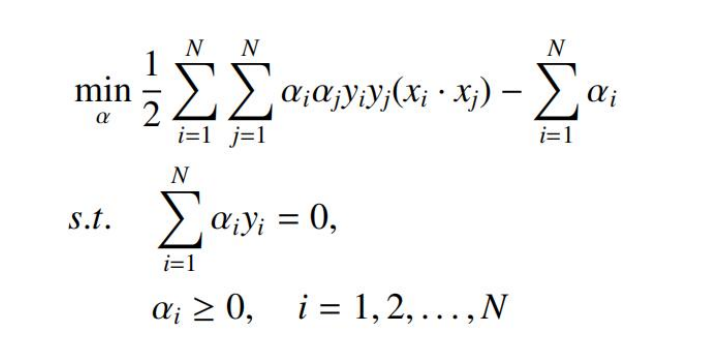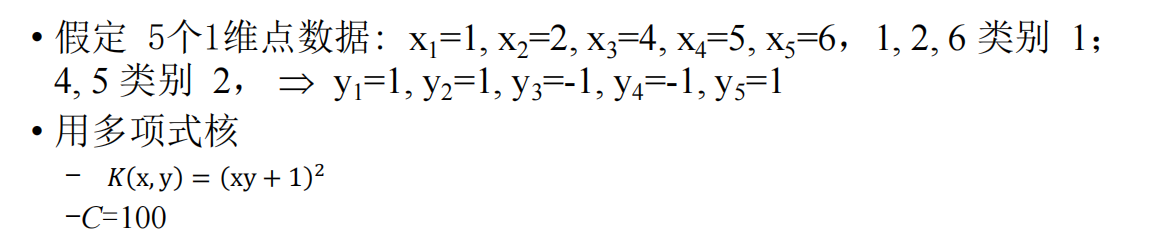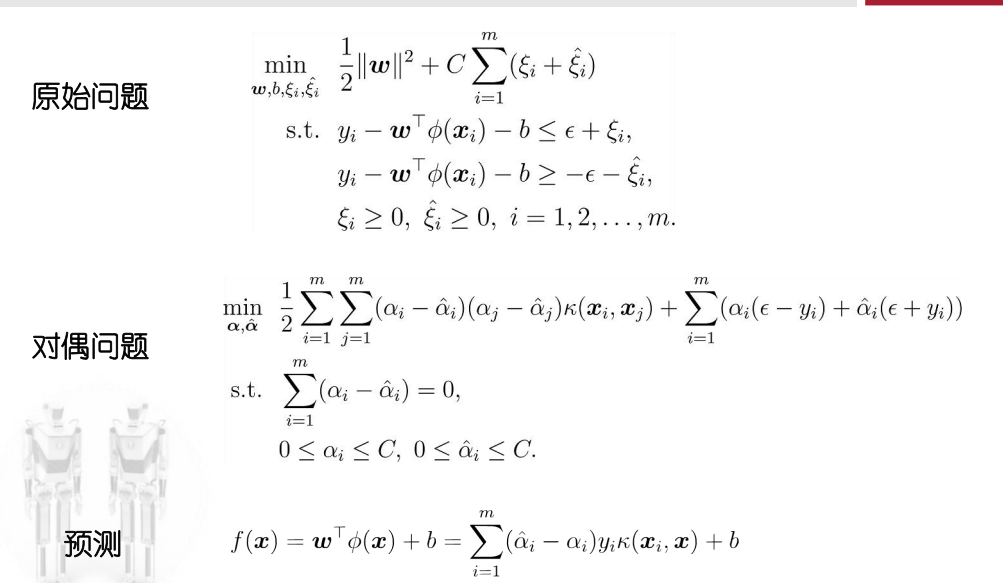机器学习第3讲——支持向量机
递进关系(from youtube)
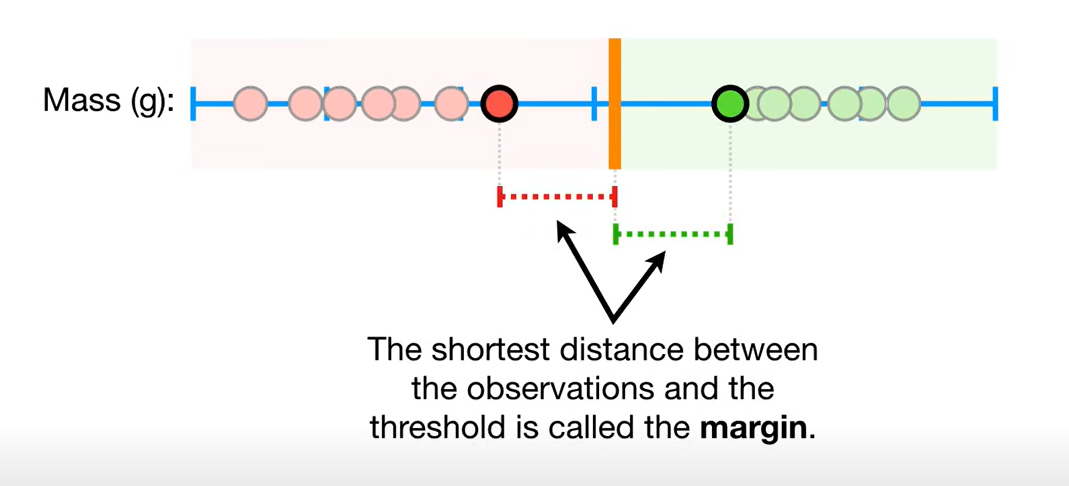
从边缘两个样本的中点划分,则margin最大(左移会使离左边变小,右移同理),这种分类为:**Maximal Margin Classifier **
但是,这种分类对训练中的异常数据非常敏感:
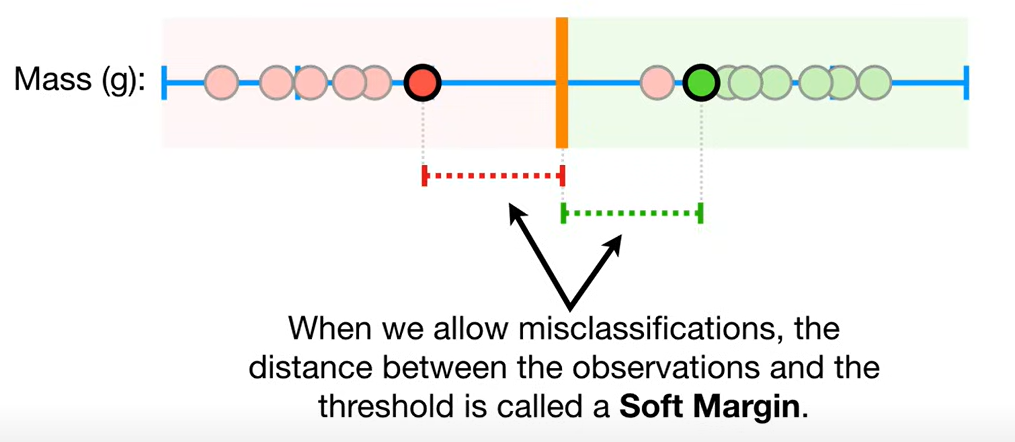
这种情况,如果允许右边一个错误分类,会在测试集上效果更好,此时margin称为Soft Margin:
使用交叉验证,以决定允许Soft Margin之间有多少个错误的分类
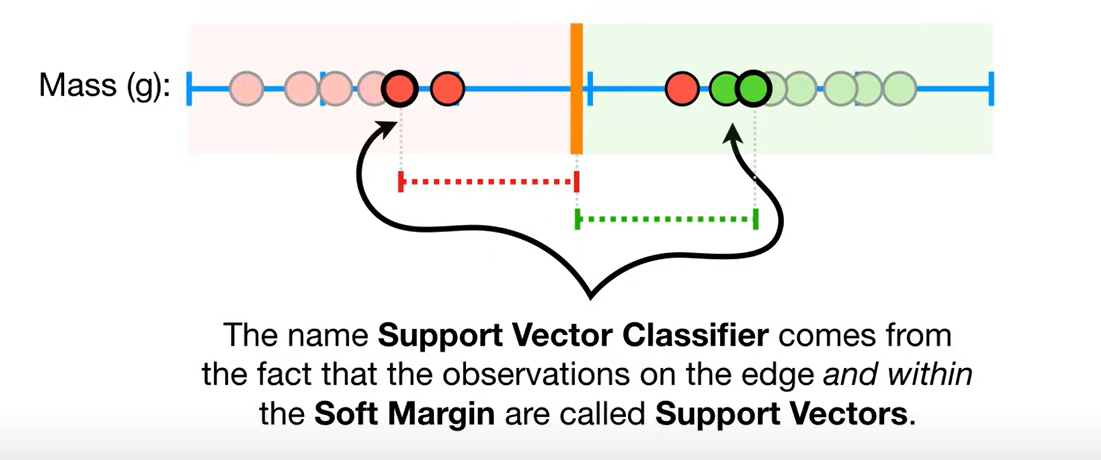
Soft Margin Classifier也称为Support Vector Classifier
边缘和soft margin之间的观察点称为支持向量:
注:PPT中将软间隔支持向量机中不是边缘的点称为软支持向量
仍然存在问题—————————————————————————————————————————————-
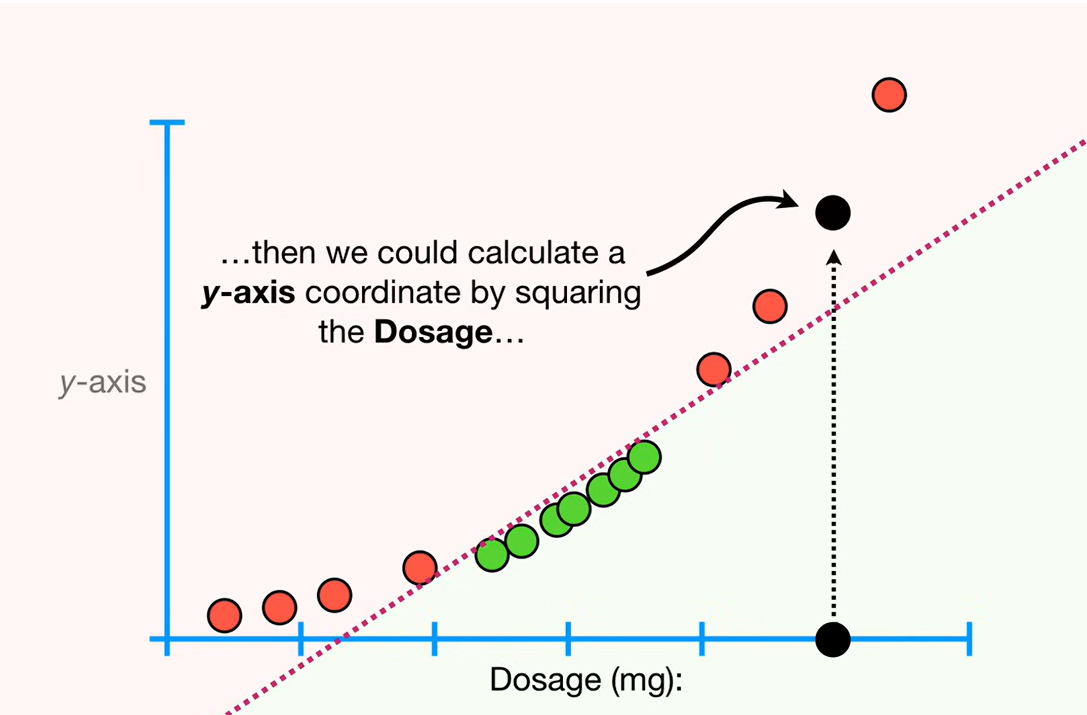
这种情况无法通过上面的方法分类
则引出支持向量机(Support Vector Machines): 将1维数据计算至2维,在2维空间找一个Support Vector Classifier
注:这里的转换并没有实际进行,通过核函数(可写成点乘的式子)在原始维度计算两两样本之间的关系,维度没变
感知机存在的问题
- 一般地,当训练数据集线性可分时,存在无穷多个分离超平面,可将两类数据正确分开;
- 感知机利用误分类样本最少的策略,求得分离超平面,不过这时的解有无穷多个;
- 线性可分支持向量机利用间隔最大化求最优分离超平面,解是唯一的。
线性可分支持向量机(linear support vector machine in linearly separable case):
训练数据线性可分时,采用硬间隔最大化,又称硬间隔支持向量机。
线性支持向量机(linear support vector machine):
训练数据近似线性可分时,通过软间隔最大化,又称软间隔支持向量机。
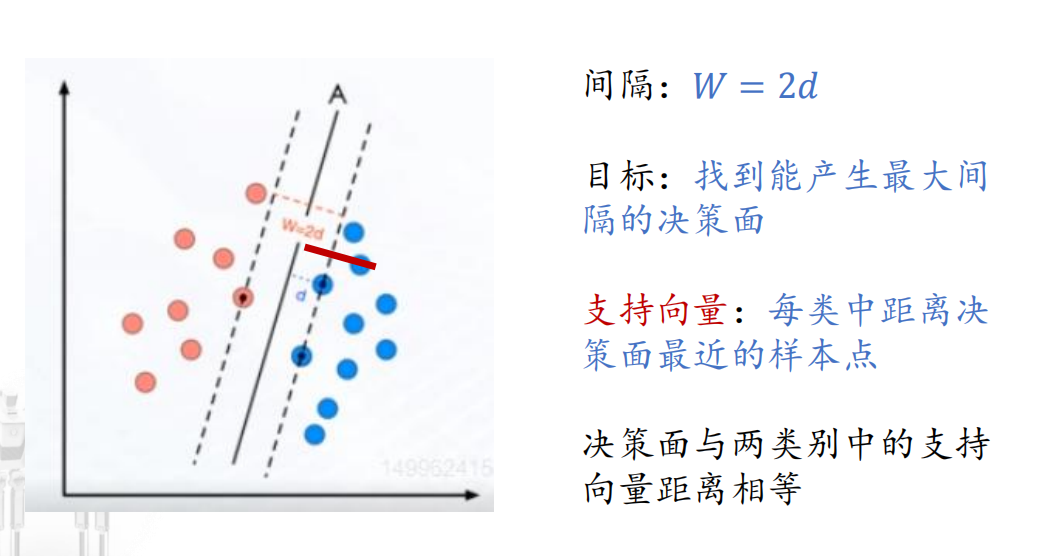
线性可分支持向量机
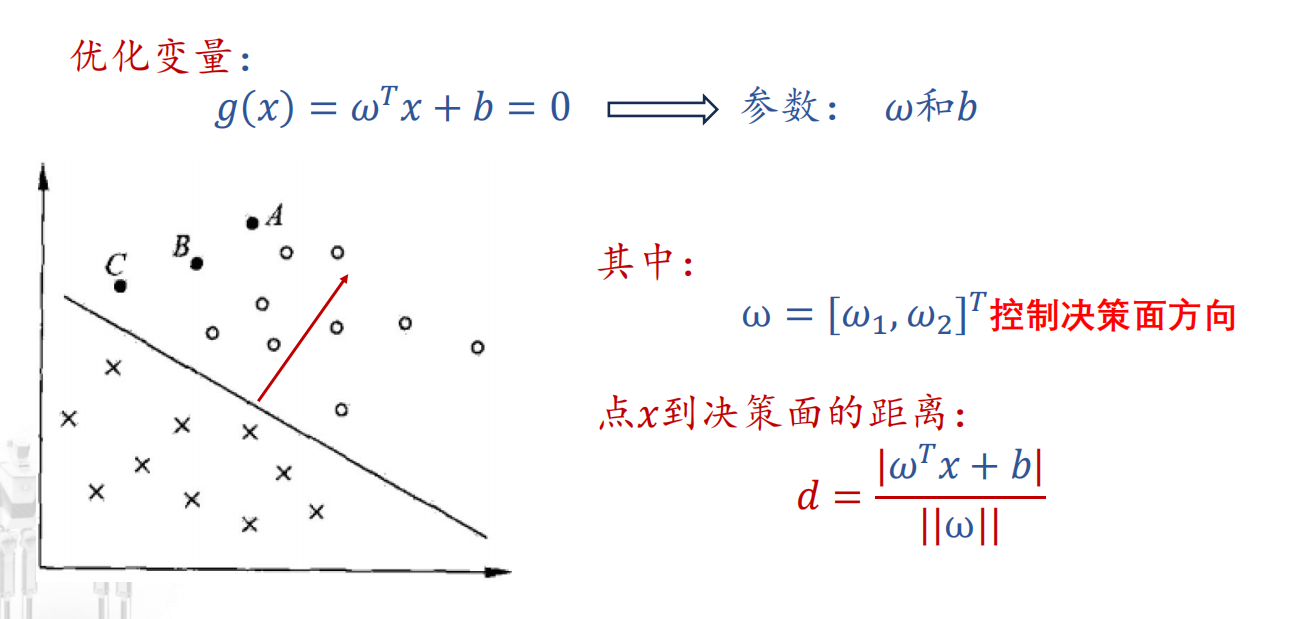
优化变量:决策面方程->如何定义?
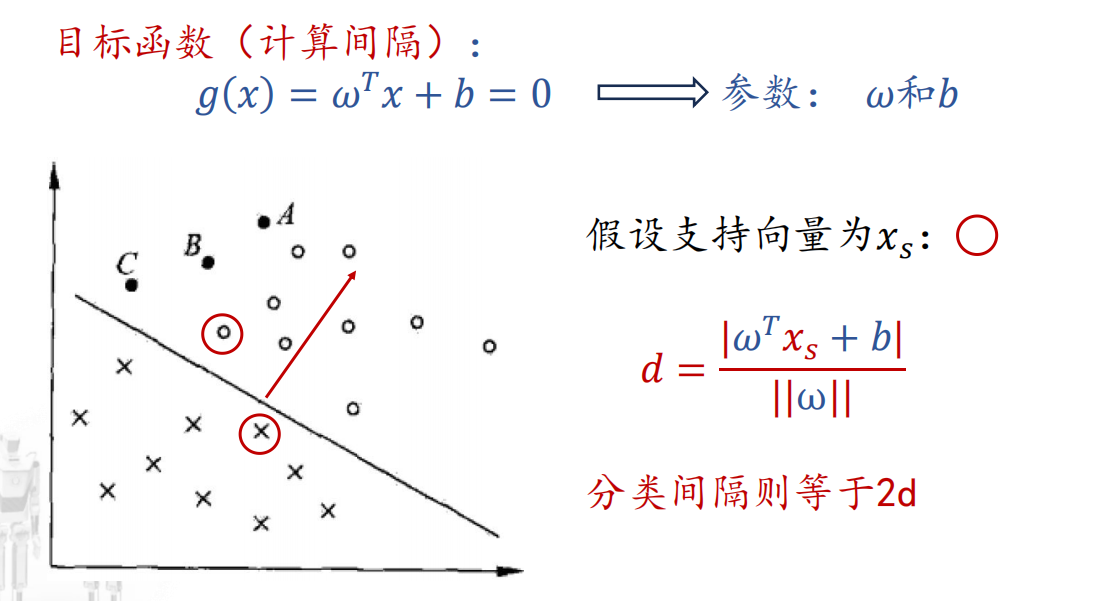
目标函数:分类间隔(最大化)->如何计算?
约束条件:所有训练样本被正确分类,如何用数学形式表达?
- 对w的约束;
- 对b的约束;
- 对支持向量(距离)的约束。
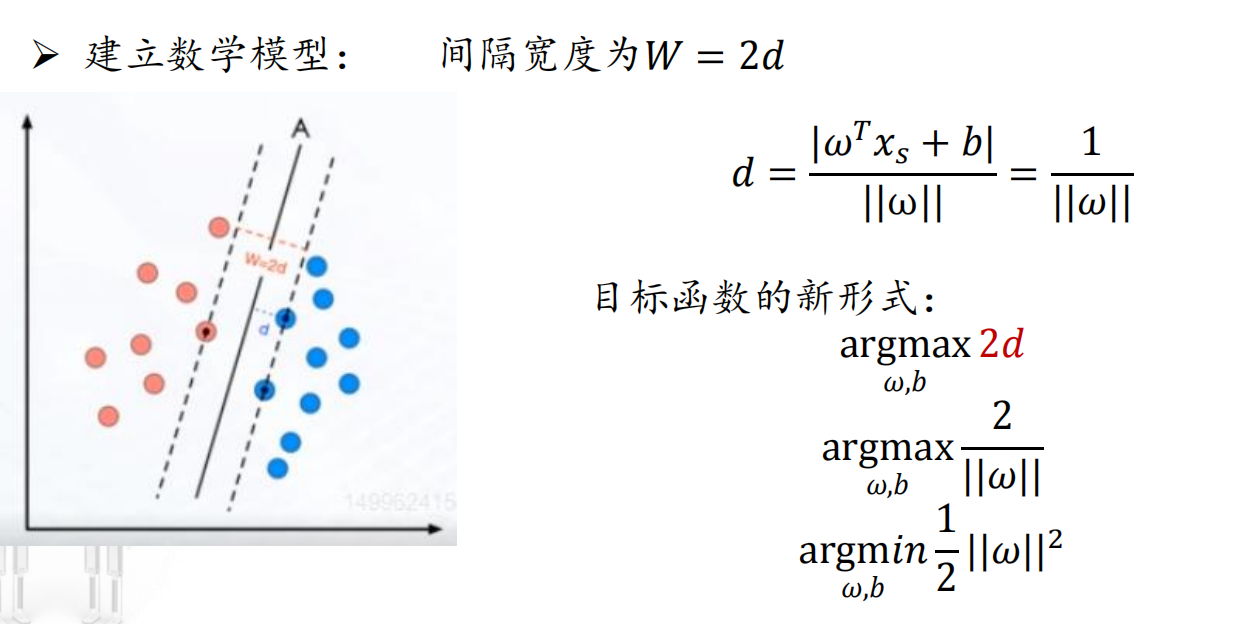
数学模型建立
得到的解对应最大间隔超平面:w*· x + b* = 0
其分类决策函数为: f(x) = sign(w*· x + b*)
小知识
- 在决定分离超平面时,只有支持向量起作用,而其他实例点并不起作用;
- 移动支持向量将改变所求的解,即改变分离超平面;
- 移动间隔边界之外的实例点,甚至去掉这些点,解是不会改变的;
- 支持向量的个数一般很少,所以支持向量机由很少的但重要的训练样本确定。
线性可分支持向量机的对偶算法(dual algorithm)
对于前面探讨得到的约束最优化问题,求解比较困难,通过数个不等式求解一个最小值的条件。
引出:利用拉格朗日对偶性(Lagrange duality),将原始问题转化为对偶问题。
前置概念
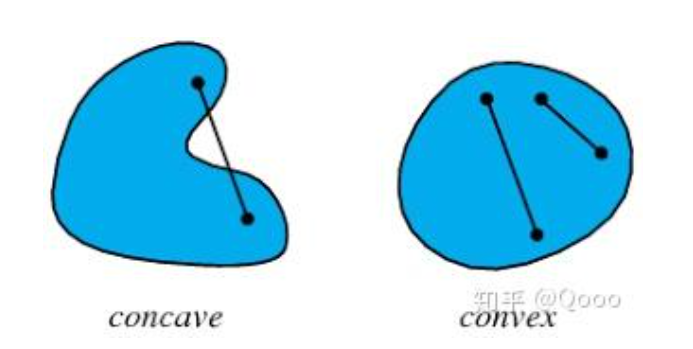
凸集(convex set): 集合中任意两点间的线段永远在集合中的集合
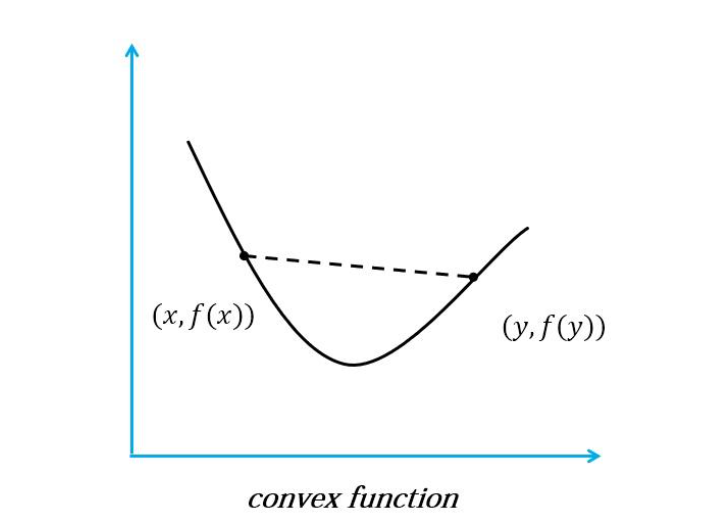
凸函数(convex function)
广义拉格朗日函数(Lagrangian)
KTT条件(Karush Kuhn Tucker)
SVM最优化问题转换为拉格朗日函数
1. 求min
这里的w,在前面知道,只有支持向量会对w有贡献;因此,如果一个向量不是支持向量,那么它的拉格朗日系数一定为0!
2. 求max
最终的对偶优化问题:
线性可分支持向量机学习算法
例题
梯度下降法
SVM中,损失函数的目标是:最小化权重,从而实现最大间隔,同时惩罚误分类样本。
线性不可分支持向量机
目标函数
个人理解:
如果松弛变量太大,约束条件是一定可以满足的,相当于一种没有约束的情况,那么这个分类器容忍的范围太大,没有意义。
因此在目标函数中引入松弛变量之和,避免它过大。
对偶算法
暂时只给出结论
梯度下降法
非线性支持向量机与核函数
核函数详见Youtube
将向量非线性映射到另外一个空间,使得样本在高维空间中线性可分。(图见开头)
核函数只以内积的形式出现,因此不需要构造一个函数进行一一映射,只需要为内积形式即可。
关于高斯核的粗略解释:
取多项式核中d=1,2,3……,并求和,得到:
a·b + a ^ 2 · b ^ 2 ……
将高斯核泰勒展开,则可得到上述结果前面再乘一个系数;
也就是高斯核可看作多项式核到无限维的映射,这里无限是因为泰勒展开
计算把x1·x2换为核函数的结果即可
小知识点
例题
多分类SVM
构造SVM多类分类器的方法主要有两类:
直接法:直接在目标函数上进行修改,将多个分类面的参数求解合并到一个最优化问题中;
计算复杂度比较高,实现起来比较困难,只适合用于小型问题中。
间接法:通过组合多个二分类器来实现多分类器的构造。
常见为one-against-one, one-against-all
one-against-one多分类
one-against-all多分类
SVM多分类模型梯度下降
支持向量回归(SVR)
传统回归:拟合训练集样本到模型f(x),通常构建损失函数,使损失函数最小化
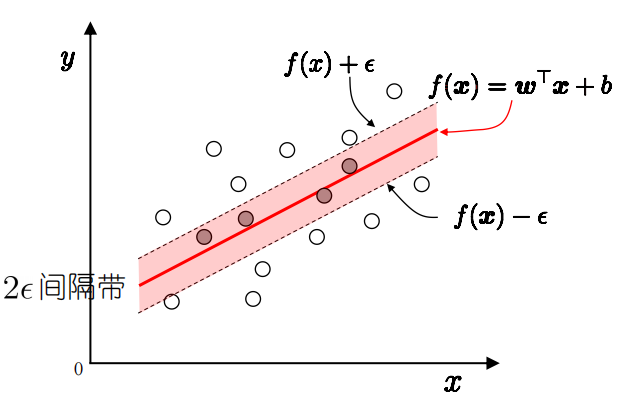
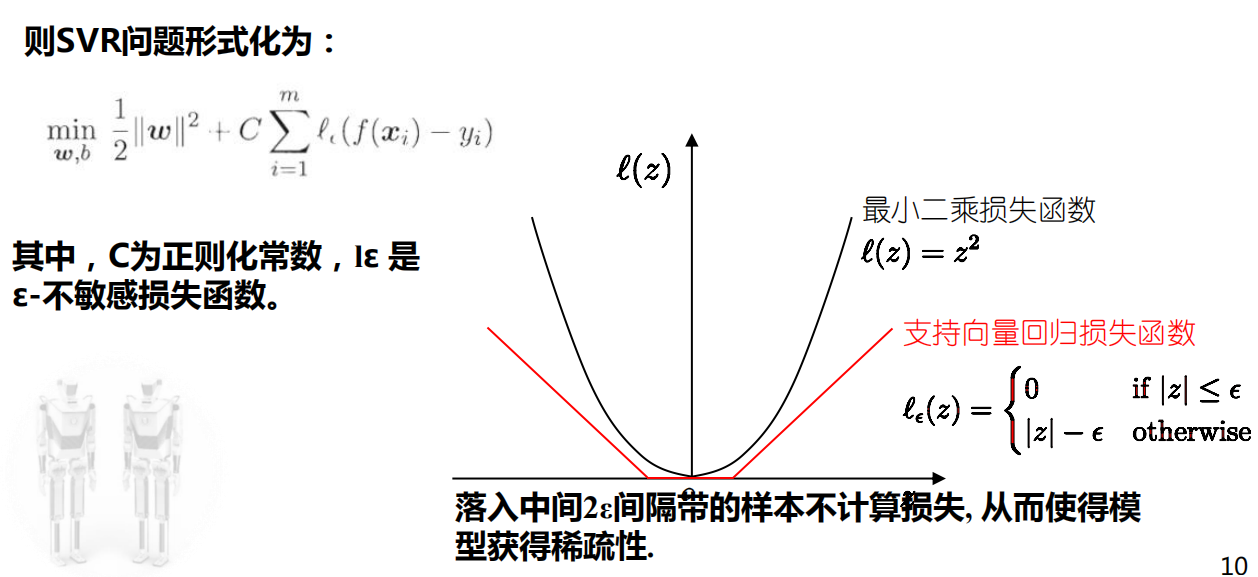
SVR:对所有的样本点,SVR能容忍回归模型f(x)与y之间存在最大偏差ε,即以f(x)为中心,构建一个宽度为2ε的隔离带。训练样本落入隔离带,则认为被预测正确
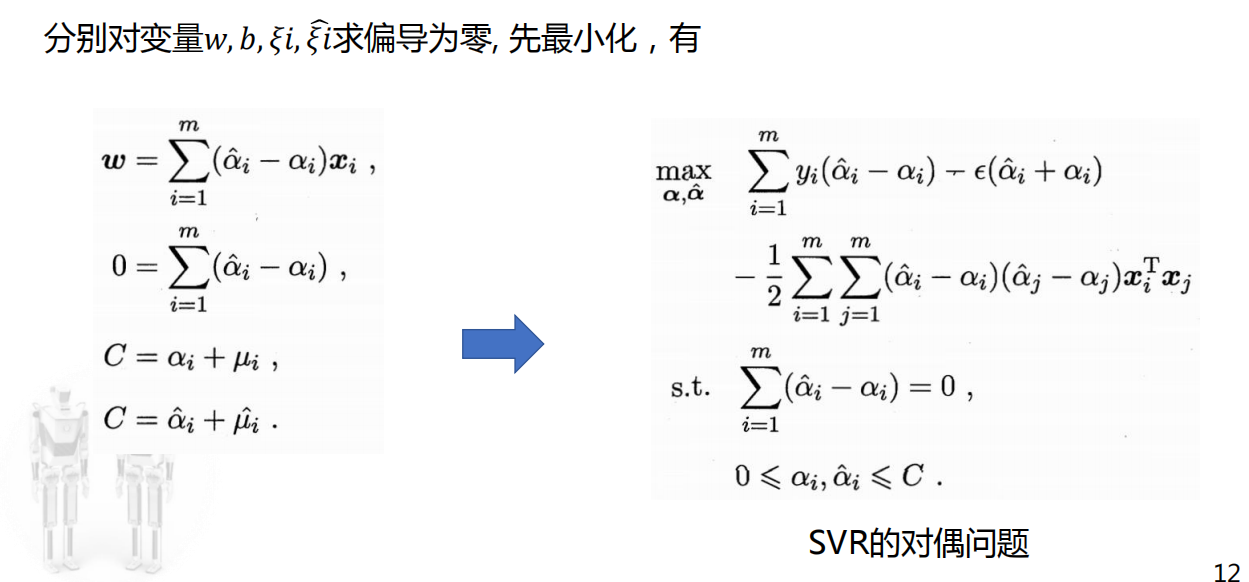
这里只需要把上一张图片中的Epsilon-不敏感损失函数带入到形式化后的目标;\n
再把这里的约束条件带入即可得到转换后的目标函数;\n
两个松弛变量意义上没什么不同,都是表示,对无法落入tube内的数据的容忍
跟前面先最小化再最大化那里类似,把求导后的零点带入拉格朗日函数即可得到化简后的最小值