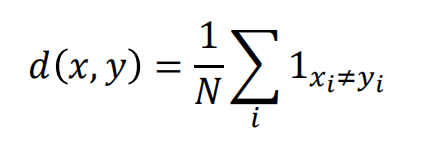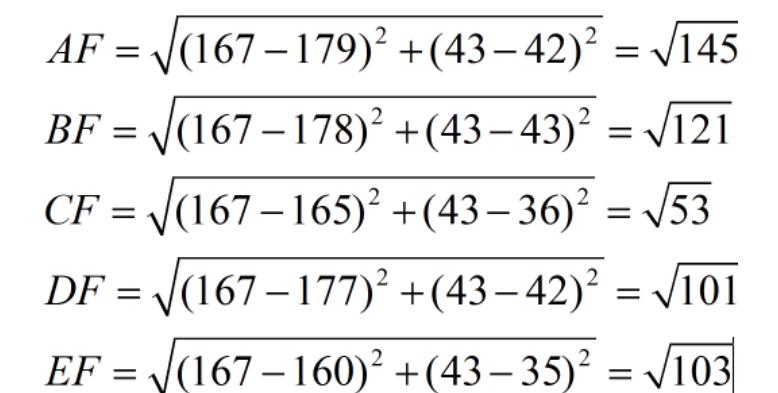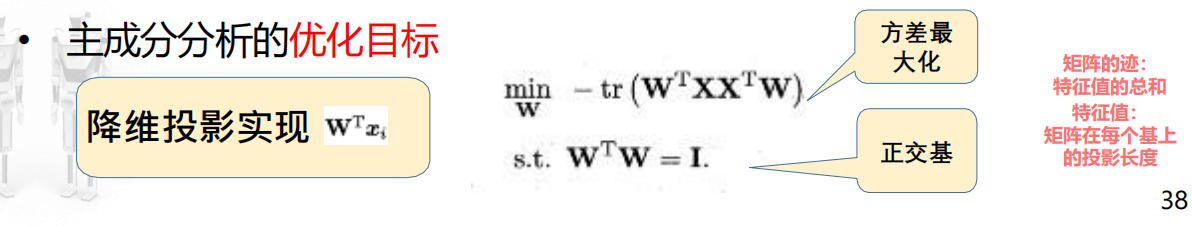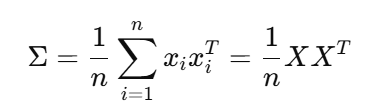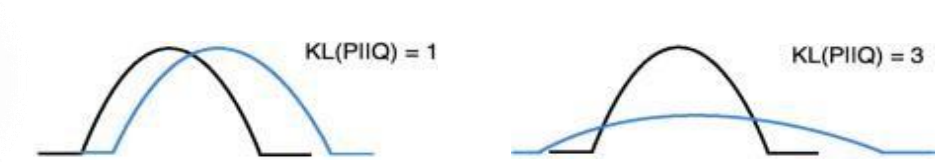Post

机器学习第5讲——K近邻

Posted Updated
By hhhi21g
13 min read
机器学习第5讲——K近邻

概述——一种基本分类和回归方法

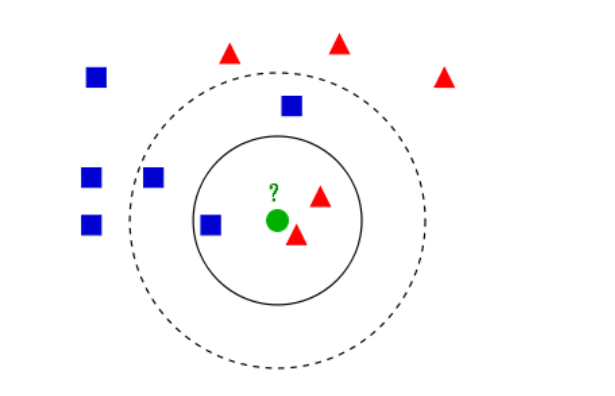
K近邻算法，即给定一个训练数据集，对新的输入实例，在训练数据集中找到与该实例最邻近的K个实例，这K个实例的多数属于某个类，就把该输入实例分类到这个类中。

alt text

  • k = 3, 选择绿圆最近的3个点，其被分为红三角；
  • k = 5, 同理，则被分为蓝方。

基本思想

  • 基于某种近邻索引方法找出训练样本集中与其最靠近的K个样本；

  • 对于分类问题使用”投票法“获得预测结果；

  • 对于回归问题使用”平均法“获得预测结果。

    有时会采用加权平均法，即：越近的邻居权重越大

基础知识

  • 急切学习: 大部分机器学习技术都有显式的训练过程，都是在训练阶段就对训练样本进行学习处理，构建起分类模型；
  • 消极学习：没有显示的训练过程，在训练阶段只是把训练样本保存起来，建模工作延迟到测试阶段才进行处理：最近邻算法

最近邻算法不是在整个样本空间上一次性地估计目标函数，而是针对每个待测样本做出局部的目标函数逼近。

当目标函数很复杂，KNN可以用不太复杂的局部函数来逼近

神经网络会尝试拟合整个函数曲线；\n

KNN不关心整条曲线长什么样,只会用非常简单的函数(投票或平均),关心测试点附近的一些样本。

K值的选取

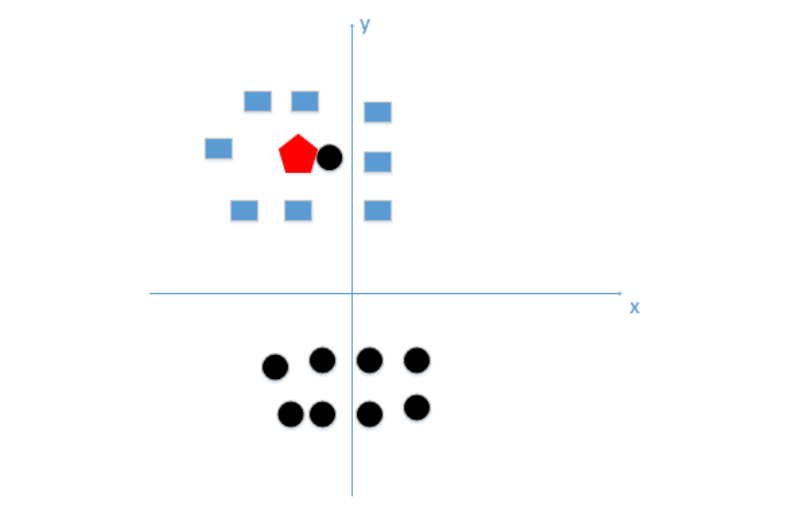
  • 如果选取较小k值，意味着整体模型会变得复杂，容易发生过拟合。

alt text

上图所示，如果k太小，很容易学习到噪声，也就非常容易判定为噪声类别(k=1:黑圆噪音，k=9:正确的蓝方)

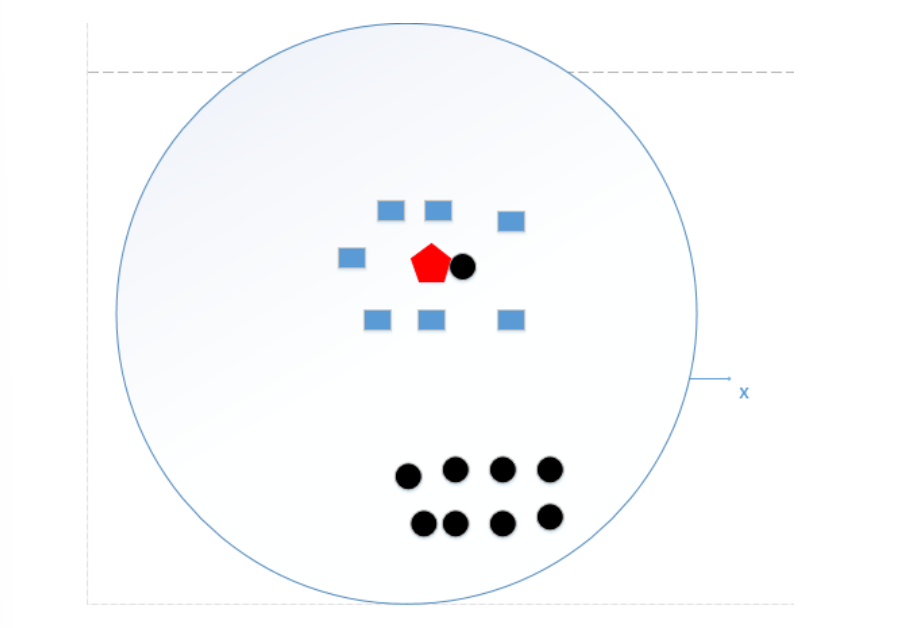
  • 如果选取较大的k值，与输入实例较远的(不相似)训练实例也会对预测起作用，意味着模型更简单

alt text

仍以该图为例，如果k=N(N为训练样本的个数)，那么无论输入实例是什么，都将简单地预测它属于在训练实例中最多的类，相当于根本没训练模型。

一般选取方式：

一般选取一个较小的数值，通常采取交叉验证法来选取最优的k值，也就是关键在调参。

距离度量

alt text

除上面三个之外：

  • 汉明距离(Hamming distance):

    alt text

​ 使用数据传输差错控制编码里面的概念：对两个字符串进行异或运算，并统计结果为1的个数，该 数即为汉明距离。

一般使用欧式距离

特征归一化的重要性

假设有5个训练样本：以身高(cm)和脚码作为特征值

A [(179,42),男] B [(178,43),男] C [(165,36)女] D [(177,42),男] E [(160,35),女]

容易发现，第一维身高特征是第二维脚码特征的4倍左右，那么在距离度量的时候，会偏向于第一维特征！

假设有测试样本F(167,43),计算欧几里得距离：

alt text

令k=3,前三个为C,D,E,预测结果为女性。

但一个女性脚码43的概率远小于男性，出现该结果的原因是什么?

由于各个特征量纲不同，这里导致身高的重要性已经远远大于脚码，这是不客观的。

也就是需要进行归一化的原因，归一化公式如下：这里算max和min只取训练集

alt text

优缺点

优：

  • 算法简单，理论成熟，既可以用来做分类也可以用来做回归；

  • 可用于非线性分类；

    即决策边界不是线性的，可能是曲线、曲面，甚至是更复杂的形状

  • 没有明显的训练过程；

  • 类域的交叉或重叠较多的待分类样本集，KNN较其他方法更为合适；

    样本分布得很杂乱，存在很多交叉、重叠、嵌套的区域

  • 该算法比较适用于样本容量比较大的类域的自动分类。

缺：

  • 需要算每个测试点与训练集的距离，当训练集较大时，计算量相当大，时间复杂度高；
  • 需要大量的内存，空间复杂度高；
  • 样本不平衡问题，对稀有类别的预测准确度低；
  • lazy learning方法，基本上不学习，导致预测时的速度比起逻辑回归之类的算法慢。

维数灾难

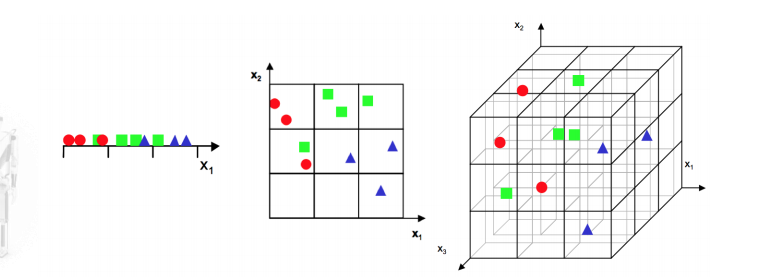
在一维的时候，数据点是非常稠密的；\n

而随着维数的增加，整个数据点的空间形成非常庞大的空间；相应的，数据分布就变得相当稀疏。

alt text

KNN的维数灾难：

KNN严重依赖距离计算，在高维情形下出现的数据样本稀疏，距离计算困难等问题是所有机器学习方法共同面临的严重障碍，被称为“维数灾难”。

缓解维数灾难的一个重要途径是降维

降维计算——线性降维

欲获得低维子空间，最简单的是对原始高维空间进行线性变换

alt text

对低维子空间性质的不同要求可通过对w施加不同的约束来实现。

降维计算——主成分分析(Principal Component Analysis, PCA)

Youtube:https://www.youtube.com/watch?v=FgakZw6K1QQ

如何用一个超平面对所有样本进行恰当的表达？

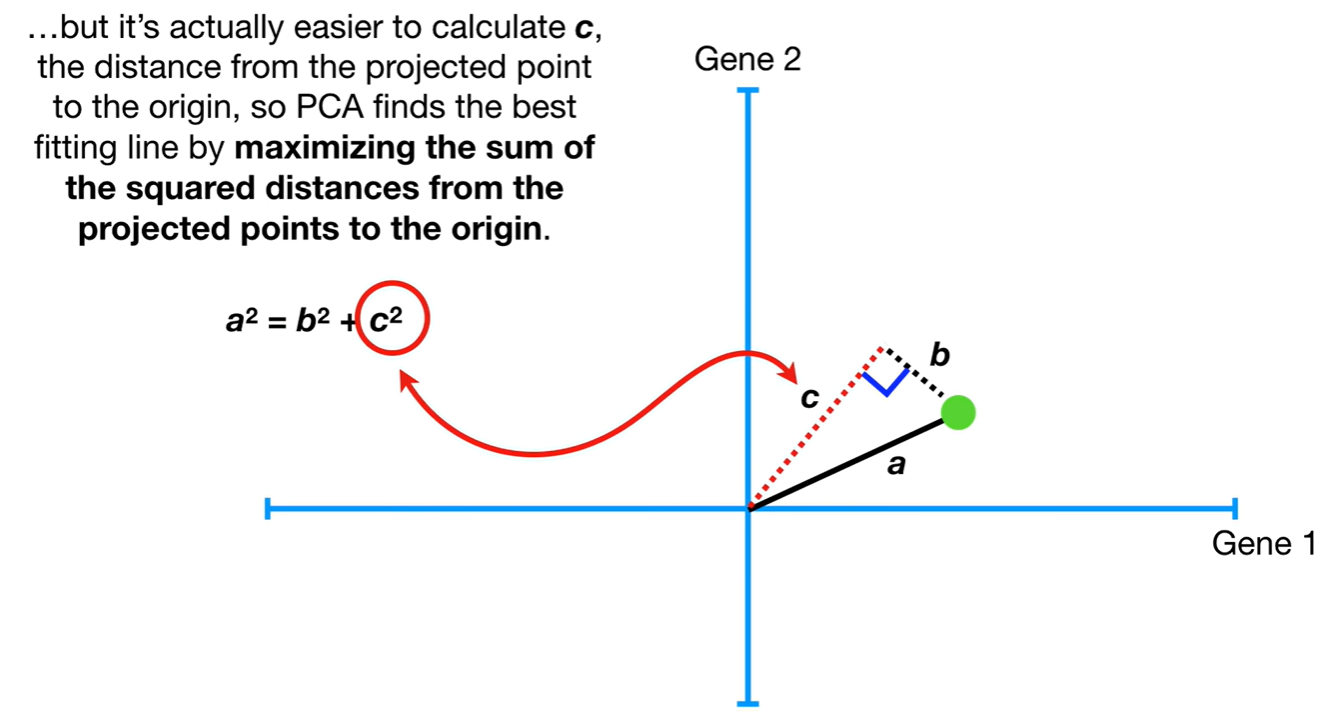
  • 最近重构性：样本点到这个超平面的距离都足够近；
  • 最大可分性：样本点在这个超平面上的投影能尽可能分开。

alt text

即：最小化b的平方

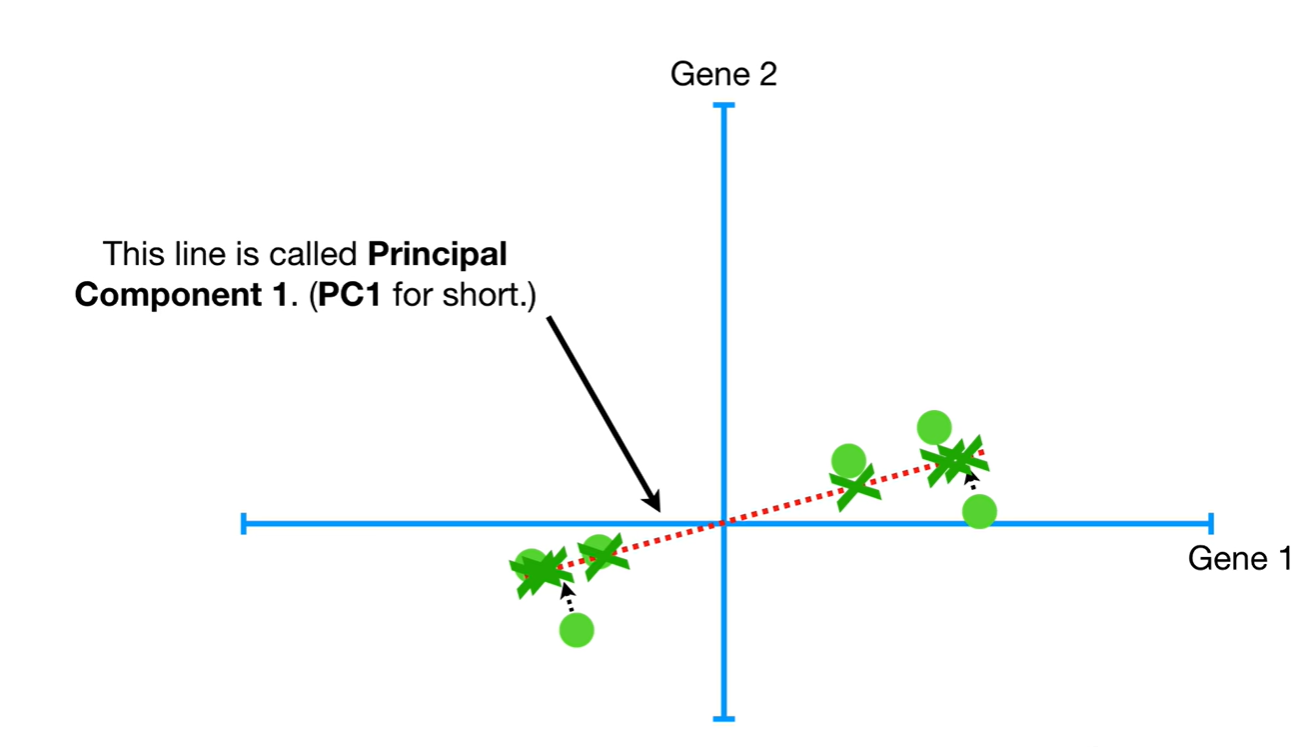
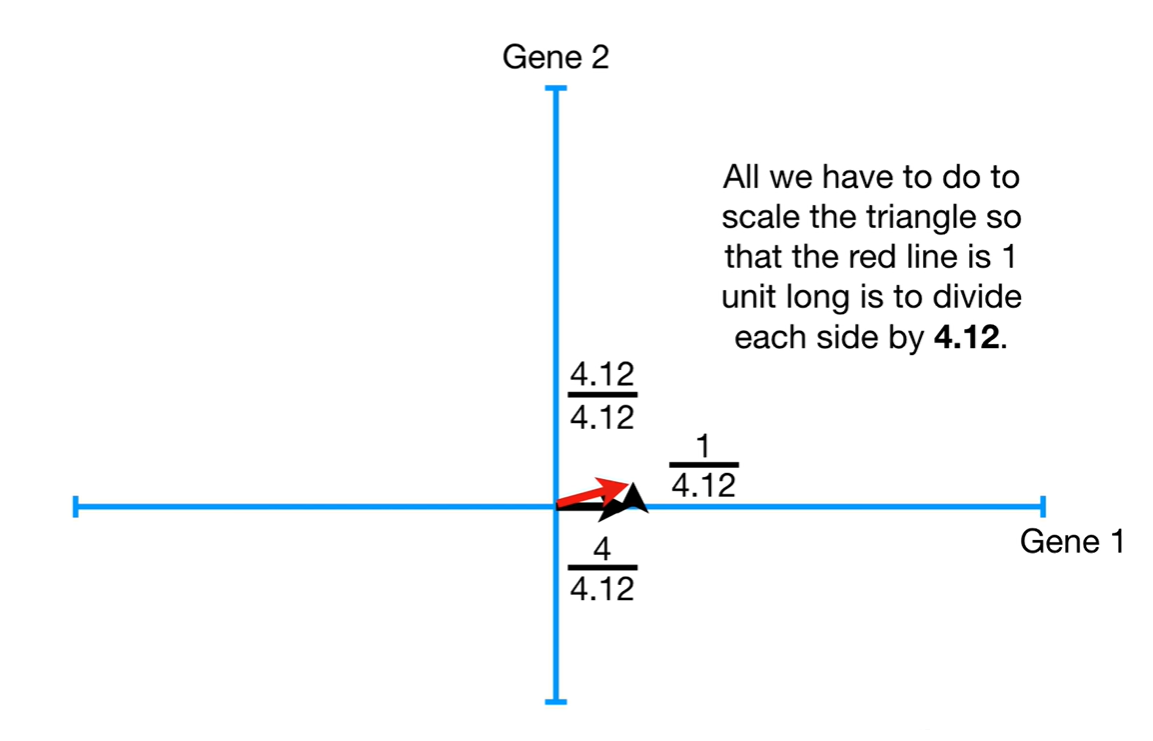
alt text

最佳拟合线(PC1)的斜率为0.25，则PC1为4部分Gene1和1部分Gene2组成

alt text

对于SVD，做了一个缩放，把红线，即样本到样本中心的距离缩为1，其余值按比例缩放。

而缩放后的这个红色向量，称为PC1的奇异向量(Singular Vector)或特征向量(Eigenvector)

alt text

  • SS的平均值：PC1的特征值(Eigenvalue)
  • SS的根号：PC1的奇异值(Singular Value)

获得正交轴后重新将点投放至新轴

即使用SVD得到PCA的方法

优化目标

alt text

简要说明：

  • W：一组”最能解释数据方差“的新坐标轴，PCA就是用这组新轴对数据进行投影和重构；

  • 若数据已经做了去中心化，即每一维的均值为0，则样本协方差的定义为：

    alt text

  • tr：计算矩阵对角线元素之和

    • 使用W进行投影后，新的协方差矩阵的对角线元素表示每个新维度的方差，因此它的迹就是低维空间中所有方向的方差之和，也就是我们关注的总信息量；
    • 希望保留的信息越多越好，因此想最大化这里的总方差。

  • XXT = I ： 投影方向之间正交，便于信息不冗余；二维上表示轴垂直。

算法描述

alt text

降维计算——t(t分布)-SNE(可视化降维)

https://www.youtube.com/watch?v=NEaUSP4YerM

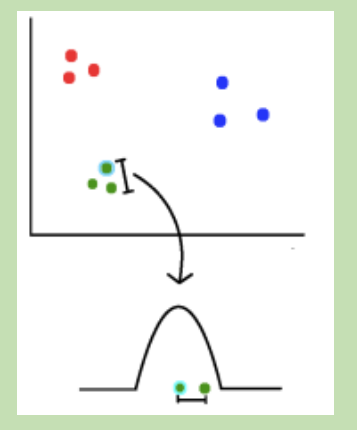
用于在二维或三维的低维空间中表示高维数据集，从而使其可视化。

  • 计算两两样本间的相似度：通过t分布曲线计算，离得越近相似度越高，越远相似度越低；需要归一化；

    alt text

    归一化用来消除比例差异。

  • 将散点随机投影到低维度；

  • 相似度高的对点吸引，相似度低的对点排斥，吸引力大于排斥力；

  • 按照吸引或排斥相应移动点，每次移动一点。

注：如果不是使用t分布，类间会离得更近

KL散度

使用KL散度来衡量低维和高维概率分布的差异，训练过程中最小化概率分布差异实现降维

KL散度越低，两个分布越接近；

KL散度为0，意味着这两个分布是相同的。

alt text

优点

效果最好的数据降维与可视化方法

缺点
  • 占内存大，运行时间长；
  • 专用于可视化，即嵌入空间只能是2维或3维；
  • 需要尝试不同的初始化点，以防止局部次优解的影响。

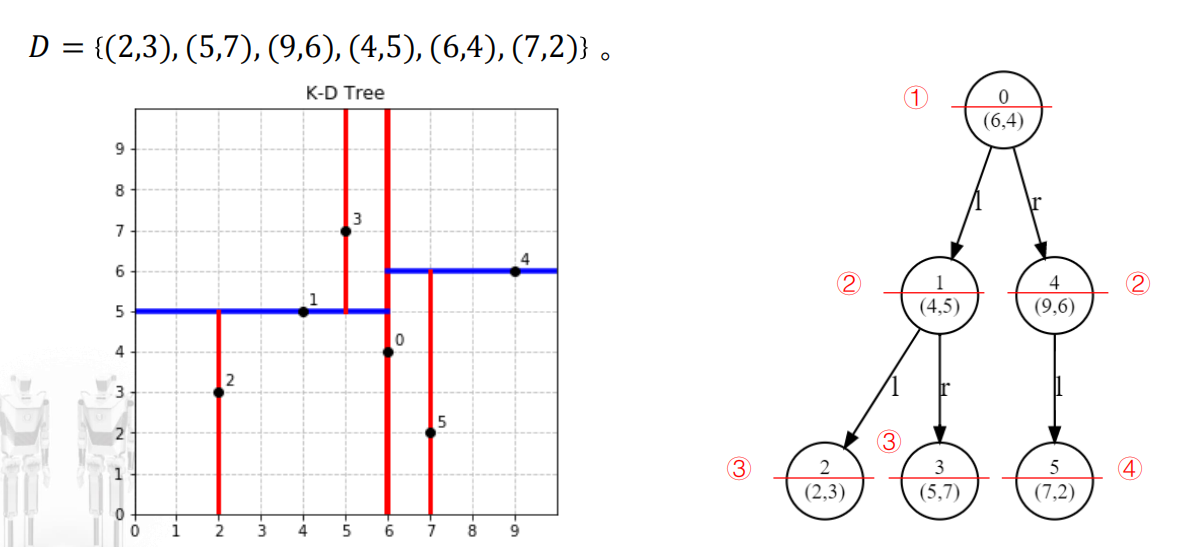
KD树(K-Dimension Tree)

  • 实现KNN算法时，主要问题是如何快速在训练样本中找到k个最近临的点；

  • 线性扫描，最简单，但在特征空间维数很高以及训练样本特别多时尤为耗时。

KD树划分

  • 从方差大的维度开始切分；
  • 取中位数作为切割点，如果样本个数是偶数个，取中间两个里面大的作为中位数；
  • 切分轴轮转，直到切后空间不包含任何点，则停止拆分。

alt text

KD树搜索

alt text

深度学习
This post is licensed under CC BY 4.0 by the author.