机器学习第6讲——聚类

概述——无监督学习中研究最多、应用最广

无监督学习：数据没有目标属性，发现数据中存在的内在结构及规律。

聚类(Clustering)是一种发现数据中的相似群(簇,clusters)的技术；是一个将数据集中在某些方面相似的数据成员进行分类组织的过程。

一个聚类就是一些数据实例的集合，这个集合中的元素彼此相似，与其他聚类中的元素不同。

聚类既可以作为一个单独过程(用于找寻数据内在的分布结构)，也可作为分类等其他学习任务的前驱过程。

分类：

• 原型聚类；
• 层次聚类；
• 密度聚类。

距离函数(相似性或相异性)：度量两个数据点的相似程度。(常用闵可夫斯基距离：K-NN中提到)

聚类任务：

• 类内差异(簇内部距离)：最小化；
• 类间差异(簇外部距离)：最大化。

性能度量：

• 外部指标：将聚类结果与某个“参考模型”进行比较；
• 内部指标：直接参考聚类结果而不用任何参考模型。

---

原型聚类

也称“基于原型的聚类”，此类算法假设聚类结构能通过一组原型刻画。

原型：样本空间中具有代表性的点

算法过程：通常情况下，算法先对原型进行初始化，再对原型进行迭代更新求解。

K均值算法

输入：簇的数目K，包含n个对象的数据集D；

输出：K个簇的集合；

• 数据：视为高维空间中的一个点，表示为向量；
• 中心点：簇的中心，反映簇的共有属性；
• 簇的数量：人为设定；
• 数据的关系度量：用“平均”的方式

方法：

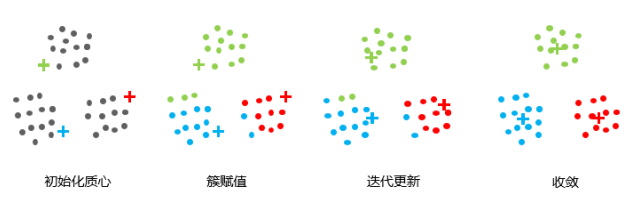
1. 选择K个点作为初始质心；
2. 将每个点指派到最近的质心，形成K个簇；
3. 对于上一步聚类的结果，进行平均计算，得出该簇的新的聚类中心；
4. 重复上述两步，直到迭代结束：质心不发生变化。

就是计算，一个点到当前所属于簇的簇K均值向量的距离的平方

---

EM实现(Expectation-Maximization)

目标：最小化J

• 初始化每个簇的均值向量；

• 重复：

  • E-步：保持μ_k不变，更新r_nk，以最小化J；
  • M-步：保持r_nk不变，更新μ_k，以最小化J；

  直到当前均值向量均未更新

只对一个μ求导，求和自然去掉

---

K值的选择

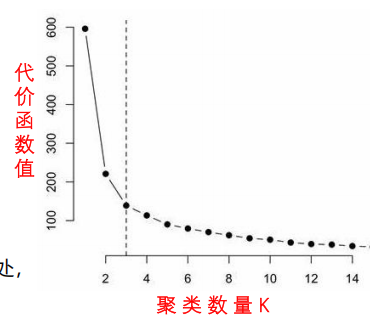
通常通过”肘部法则“进行计算，在一个肘点后，代价函数的值就会下降得非常慢，因此选择肘点。

存在问题：

• K-均值可能会停留在一个局部最小值处，而这取决于初始化的情况；

• 为解决该问题，通常需要多次运行K-均值算法，每一次都重新进行随机初始化，最后再比较多次运行K-均值的结果，选择代价函数最小的结果。

---

中心点

一般采用随机初始化，后续设置为簇内数据的平均向量。

初始中心如何选择？

• 多次运行：效率较低，看运气；
• 采少量样本，借助其他聚类，先确定初始中心：开支大，仅适用于K较小的情况；
• 初始选择大于K的数量，从中挑选聚类分隔较为明显的中心；
• 后处理”修补“聚类的结果；
• 二分K均值方案(Bisecting K-means)

二分K均值方案：

• 不容易受到初始化问题的影响；
• 基本思想：为了得到K个簇，先分为2个簇，然后不断选择其中一个分裂。

---

优点与问题

优点：

• 原理简单，实现容易，收敛速度快；
• 聚类效果较优；
• 算法的可解释度比较强；
• 主要需要调参的参数仅仅是簇数K

缺点：

• 当出现不同规模的簇时，往往结果会受到一定干扰；

• 当出现密度不同的簇时，。。。。。。。
• 当出现不规则形状的簇时(非球状)，往往很难有效聚类(小簇合成大簇)；

---

基于高斯混合模型(Mixture of Gaussian)的聚类实现

采用概率模型来表达聚类原型

多元高斯分布

似然函数

最大似然法

高斯混合聚类算法

类似于EM算法

• 先随机初始化高斯分布；
• 将点按比例标记离得更近的高斯；
• 再忽略上一个高斯，只根据点的标记新建高斯；
• 重复进行，直至不变或收敛。

---