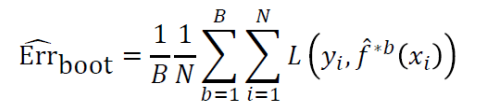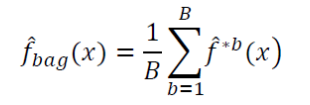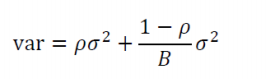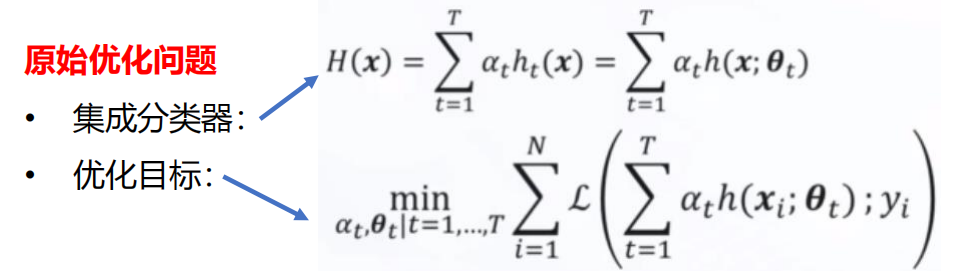机器学习第9讲——集成学习
集成学习
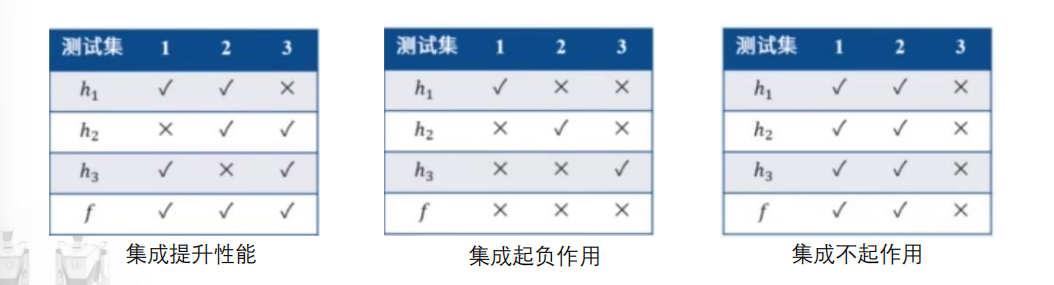
- 考虑一组预测模型h1,…hl
- 不同的预测模型在数据上具有不同的表现；
- 成功的集成需要多样性
- 预测模型应该犯的错误不相同；
- 鼓励把不同类型的预测模型集成在一起。
组合模型
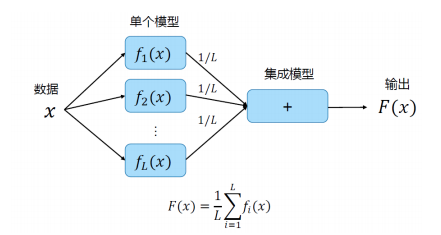
平均
回归问题求平均值，分类问题进行投票
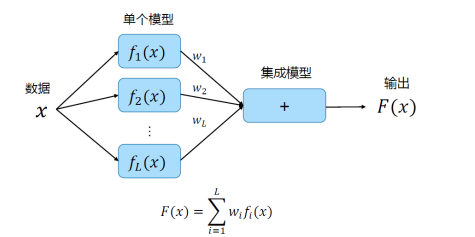
加权平均
训练集成模型时更新所有模型
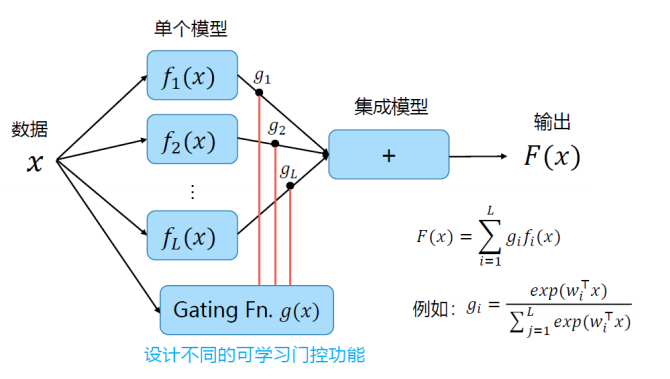
门控
训练集成模型时更新所有模型
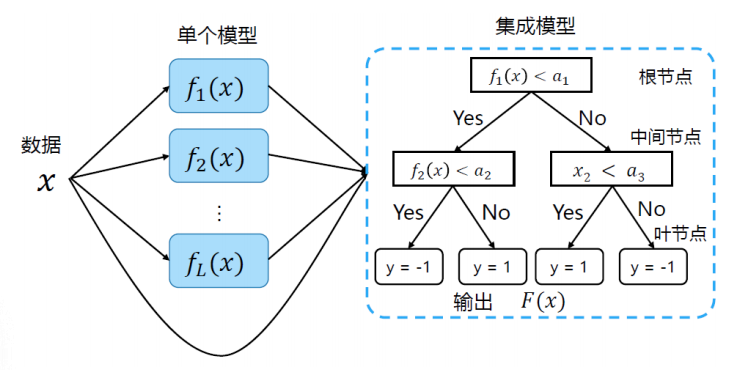
树模型
用决策树作为集成模型，根据x和f函数的值进行结点拆分
常见名词
- 个体学习器：参与集成的学习器单元；
- 同质：个体学习器类型相同；
- 异质：个体学习器类型不同；
- 基学习器：“同质”的个体学习器；
- 组件学习器：“异质”的个体学习器；
- 强学习器：预测结果明显比随机猜测好的学习模型；
- 弱学习器：预测结果比随机猜测略好的学习模型；
弱学习器设计规则
- 好：至少为弱学习器；
- 不同：不同个体学习器的预测结果存在多样性。
Bagging方法
Bagging策略
Bagging: 并行学习，从原始样本集中生成不同的子集
如何生成子集？
- 若子集与原始集合偏离过多，则基学习器经验风险过大；
- 若两个子集的重叠样本过多，则基学习器将过于相似；
采样方法
Bootstrap: 有放回的均匀采样
未被抽到的样本可作验证集；
Pasting: 无放回的均匀抽样
个体分类器的训练样本数量一般为总样本的60-80%，无重复。
Bagging vs. Boosting
- bagging: 自举法
- 个体学习器并行学习，学习过程相互独立；
- 如何保证不同：个体学习器采用不同训练集
- boosting: 提升法
- 个体学习器串行学习，集成性能逐步提升；
- 如何保证不同：个体学习器对训练样本加以不同权重
Bootstrap(自举法)
- 每一个复制数据集的大小都和训练集的大小相同；
- 在复制数据集上进行统计数值的评估分析
如果直接使用整个训练数据来评估模型：
由于数据实例在自举采样数据集中的概率为：0.632(1-1/e)
如果直接在训练集上验证，大概率会过拟合：
- 例如，正确的错误率：0.5；
- 利用自举法错误率：0.632*0 + (1 - 0.632)*0.5 = 0.184
Leave-One-Out Bootstrap(留一自举法)
当构建自举复制集时不采样实例i，然后利用实例i来评估模型
Bootstrap Aggregating
对一个有n个训练样本的数据集Z，通过有放回地采样n个实例构造得到新的训练集Z*;
构造B个自举采样集Z*b;
训练一个预测模型集合；
在预测结果上求平均值：
为什么有效?
Bagging有效的原因是与原始模型相比偏差相同但是降低了方差
对低偏差和高方差的预测模型尤其有效果。
如果有一系列服从同一分布的变量，两两之间的关联性为ρ，对变量值取平均之后的方差为：
如果采样样本无限大，该公式的值会降为ρσ2
用自举采样的数据进行训练得到的模型很可能是有一定相关性的：
随机森林
随机森林和bagging算法的主要区别在于构建一个解耦合(decorrelated)的树，然后对结果取平均
- 在每个树节点分裂前，随机选择m <= p个特征作为分裂的候选变量
- 一般m = 根号p，甚至取值为1
加性模型(Additive Models)
Boosting方法
串行、逐个增加个体学习器，逐步提升集成学习系统的性能
提升的思路：
- 串行训练个体学习器；
- 新增加的个体学习器重点关注错分的样本；
设计方向：
- 提升基学习器的泛化性能；
- 增强基学习器的多样性；
算法思路：
- 前向分布优化：逐步增加个体学习器，分解简化优化问题；
- 重赋值(Reweighting): 在学习目标中增加错分样本的权重。
挑战：
- 可能存在多个局部最优解，解的鲁棒性难以保障；
- 参数数量多，梯度形式复杂，通常没有封闭解；
- 梯度下降法的收敛速度难以保障；
- 基分类器的泛化性能和“好而不同”的设计目标难以保障
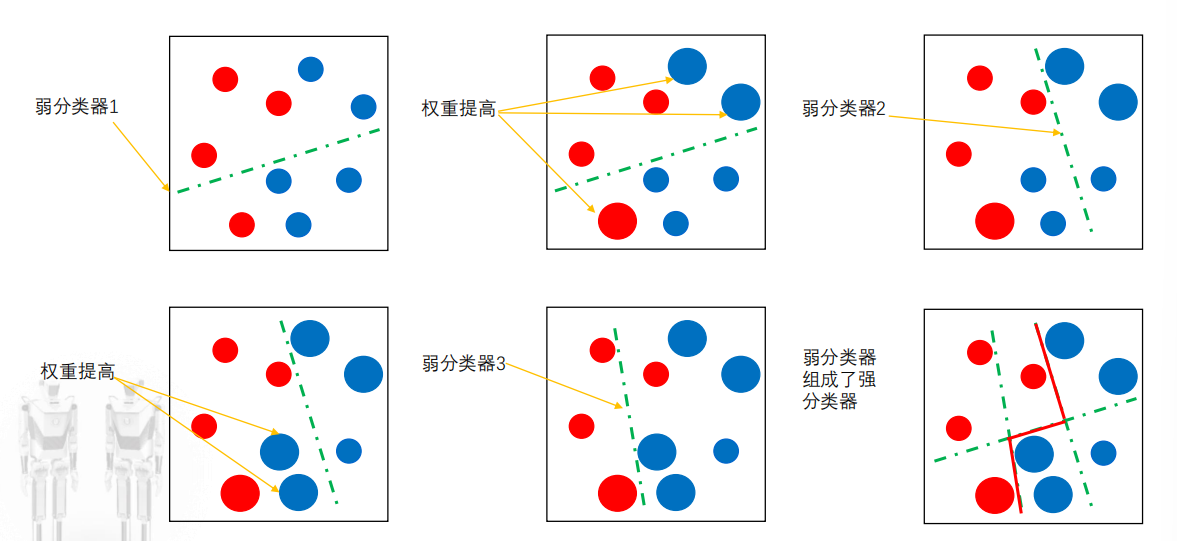
Adaboost算法
Adaptive Boosting (自适应增强)，其自适应在于：前一个基本分类器分错的样本会得到加强，加权后的全体样本再次被用来训练下一个基本分类器。同时，在每一轮中加入一个新的弱分类器。直到达到某个预定的足够小的错误率或达到预先指定的最大迭代次数。
后一个模型的训练永远是在前一个模型的基础上完成
算法思想
- 初始化训练样本的权值分布，每个样本具有相同权值；
- 训练弱分类器：
- 如果样本分类正确，则在构造下一个训练集中，它的权值就会被降低；
- 反之提高；
- 用更新过的样本集去训练下一个分类器；
- 将所有弱分类器组合成强分类器，各个弱分类器的训练过程结束后，加大分类误差率小的弱分类器权重，降低分类误差率大的弱分类器的权重。
符号定义
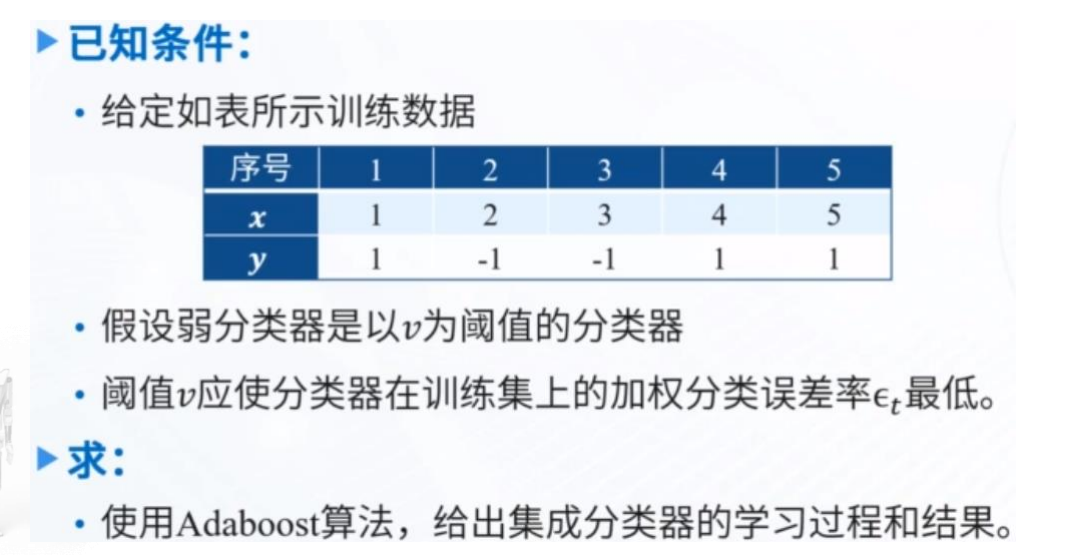
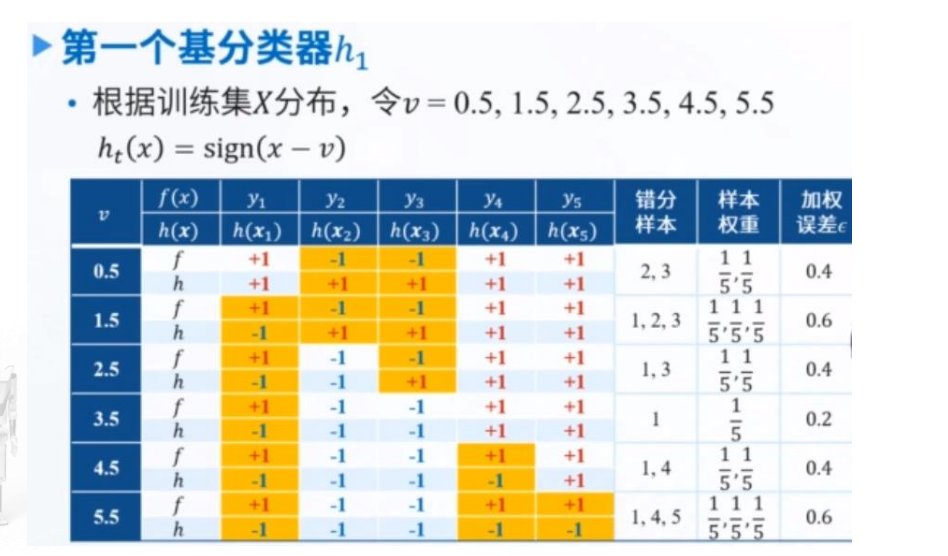
例子PPT49
