Code06-动态规划

Code06-动态规划(洛谷[动态规划1]题单)

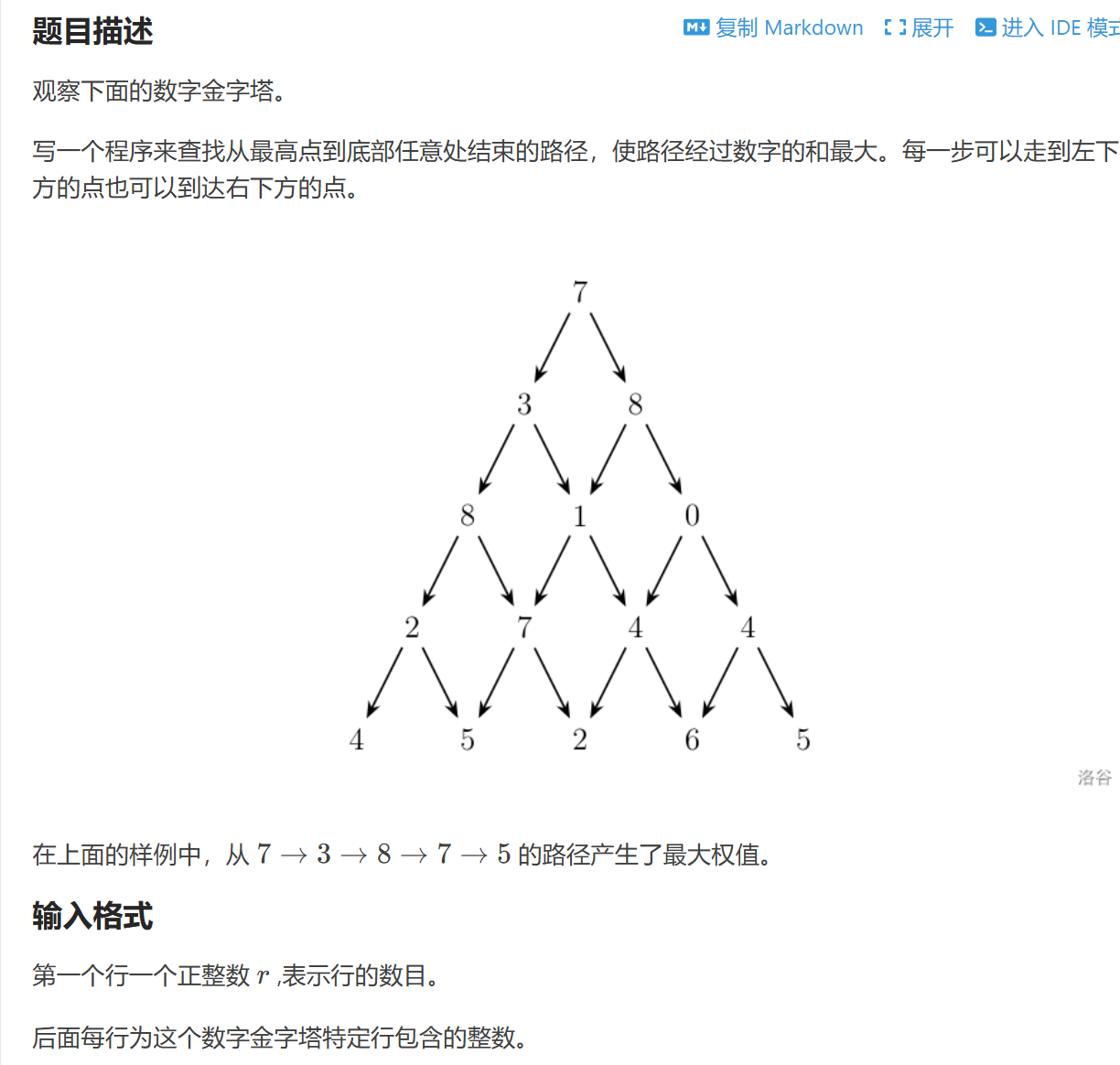
洛谷 P1216

package luogu;

import java.util.Scanner;

public class P1216 {

	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);
		int r = sc.nextInt();
		int[][] h = new int[r][r]; 
		int[] dp = new int[r]; // 只存当前层的最大路径和，避免 MLE

		for (int i = 0; i < r; i++) {
			for (int j = 0; j <= i; j++) {
				h[i][j] = sc.nextInt();
			}
		}
		sc.close();

		// 复制最后一行到 dp，作为初始值
		System.arraycopy(h[r - 1], 0, dp, 0, r);

		for (int i = r - 2; i >= 0; i--) {
			for (int j = 0; j <= i; j++) {
				dp[j] = Math.max(dp[j], dp[j + 1]) + h[i][j];
			}
		}

		System.out.println(dp[0]);
	}
}

思路：

简单的动态规划，状态转移方程容易写出，没能选择dp的恰当含义，且没有使用滚动数组减小内存

• dp[i][j]:第i层j位置到达最底层的最长路径；

  h[i][j]:i,j位置的数值；

  • 对于最底层，有dp[i][j] = h[i][j], 即边界

• 状态转移方程：这里所求为dp[0][0], 而最底层dp值已知，因此自底向上递归

  dp[i][j] = max{dp[i+1][j], dp[i+1][j+1]} + h[i][j]

• 滚动数组的加入：

  直接使用二维数组会出现MLE，分析可知，dp[i][j]只与dp[i+1][j]和dp[i+1][j+1]两个值有关；

  且dp[i+1][j]在这一层的计算中的后面并不会再被使用；

  • 因此，可以用dp[i][j]覆盖dp[i+1][j],依次覆盖下去，则dp可简化至一维数组。

---

洛谷 P1048

package luogu;

import java.util.Scanner;

public class P1048 {

	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);
		int t, m;
		t = sc.nextInt();
		m = sc.nextInt();
		int[][] task = new int[m][2];

		for (int i = 0; i < m; i++) {
			task[i][0] = sc.nextInt(); // 采集所需时间
			task[i][1] = sc.nextInt(); // 价值
		}
		int[] dp = new int[t + 1];
		for (int i = 0; i < m; i++) {
			for (int j = t; j >= task[i][0]; j--)
				dp[j] = Math.max(dp[j], dp[j - task[i][0]] + task[i][1]);
		}

		System.out.print(dp[t]);
	}
}

思路：

0-1背包问题：

• dp[i][j]:处理好前i株草药，剩余时间为j，能够采集的最大价值；

  dp[i][j] = max{dp[i-1][t],dp[i-1][t-tj] + vj}

• 处理好前i株草药可以通过循环表示，降维至一维数组；

• 需要倒序遍历，防止选中新更新的状态。

---

洛谷 P2196

package luogu;

import java.util.Arrays;
import java.util.Deque;
import java.util.LinkedList;
import java.util.Scanner;

public class P2196 {

	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);
		int n = sc.nextInt();
		int[] v = new int[n + 1];
		for (int i = 1; i <= n; i++) {
			v[i] = sc.nextInt();
		}

		int[][] h = new int[n + 1][n + 1];
		for (int i = 1; i < n; i++) {
			for (int j = 1; j <= n - i; j++) {
				h[i][j + i] = sc.nextInt();
			}
		}

		int[] dp = new int[n + 1];
		int[] pre = new int[n + 1];

		int maxNum = 0;
		int index = 1;

		Arrays.fill(pre, -1);

		for (int i = 1; i <= n; i++) {
			dp[i] = v[i]; // 初始值为自身价值
			pre[i] = -1;

			for (int k = 1; k < i; k++) {
				if (h[k][i] == 1 && dp[k] + v[i] > dp[i]) {
					dp[i] = dp[k] + v[i];
					pre[i] = k; // 记录前驱
				}
			}

			if (dp[i] > maxNum) {
				index = i;
				maxNum = dp[i];
			}
		}

		// 回溯路径
		Deque<Integer> path = new LinkedList<>();
		while (index != -1) {
			path.push(index);
			index = pre[index];
		}

		while (!path.isEmpty()) {
			System.out.print(path.pop() + " ");
		}
		System.out.println();
		System.out.println(maxNum);
	}
}

思路：

• h[i][j]:地窖i是否能够去到地窖j；

  dp[i]:在地窖i位置，已经挖得的地雷数目；

• 状态转移方程：

  对于每个地窖i：

  for j in range[1,5]:
      dp[i] = max{dp[j] if(h[j][i-j] == 1)} + v[i]
  

• 存储路径：

  这里由状态转移方程可知，

  • 对于每一个地窖，都是先求其能够连接到的前一个地窖位置所能挖出的地雷数；

  • 换而言之，得到每个地窖i的dp值时，只能够得到这条路径在它前面一个的地窖序号；

  • 将该序号存为pre[i], 初始化为-1,表示没有前序序列；

• 无论是单个地窖还是全局，存储最大地雷数的路径仅存数目与对应序号；

• 回溯路径：

  通过pre数组回溯，直至值为-1，即没有前序序列；

• 使用栈进行管理

注意：

• Arrays.fill(): 用于将一个数组的所有元素填充为指定的值；

  Arrays.fill(pre, -1);
  

• Java中队列与栈的标准库接口。

---

洛谷 P1164

package luogu;

import java.util.Scanner;

public class P1164 {

	static int resCnt = 0;

	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);
		int n, m;
		n = sc.nextInt();
		m = sc.nextInt();
		int[] v = new int[n];
		for (int i = 0; i < n; i++) {
			v[i] = sc.nextInt();
		}
		sc.close();

		int[] dp = new int[m + 1]; // dp[j]:凑成金额j的方案数
		dp[0] = 1;

		for (int i = 0; i < n; i++) {
			for (int j = m; j >= v[i]; j--) {
				dp[j] += dp[j - v[i]];
			}
		}
		System.out.print(dp[m]);
	}
}

思路：

• dp[j]: 凑成金额j的金额数；

• 问题即为求解dp[m];

• 遍历每种菜品，逆序更新方案数：

  根据状态转移方程：dp[j] += dp[j-v[i]]

---

洛谷 P3842

package luogu;

import java.util.Scanner;

public class P3842 {

	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);
		int n = sc.nextInt();

		int[][] lr = new int[n + 1][2];
		for (int i = 1; i <= n; i++) {
			lr[i][0] = sc.nextInt();
			lr[i][1] = sc.nextInt();
		}

		int[][] dp = new int[n + 1][2];
		dp[1][0] = lr[1][1] - 1 + lr[1][1] - lr[1][0];
		dp[1][1] = lr[1][1] - 1;
		for (int i = 2; i <= n; i++) {
			dp[i][0] = lr[i][1] - lr[i][0] + 1 + Math.min(dp[i - 1][0] + Math.abs(lr[i][1] - lr[i - 1][0]),
					dp[i - 1][1] + Math.abs(lr[i][1] - lr[i - 1][1]));
			dp[i][1] = lr[i][1] - lr[i][0] + 1 + Math.min(dp[i - 1][0] + Math.abs(lr[i][0] - lr[i - 1][0]),
					dp[i - 1][1] + Math.abs(lr[i][0] - lr[i - 1][1]));
		}
		int res1 = dp[n][1] + Math.abs(n - lr[n][1]);
		int res2 = dp[n][0] + Math.abs(n - lr[n][0]);
		int res = res1 > res2 ? res2 : res1;
		System.out.print(res);
	}
}

思路：

• dp[i][0]:走完第i行停到左端点的最短路径；

  dp[i][1]:走完第i行停到右端点的最短路径；

• 状态转移方程：

  如上代码中循环部分

---

洛谷 P1049

package luogu;

import java.util.Scanner;

public class P1049 {

	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);
		int v = sc.nextInt();
		int n = sc.nextInt();
		int[] vol = new int[n + 1];

		int[][] dp = new int[n + 1][v + 1];
		for (int i = 0; i < n; i++) {
			vol[i] = sc.nextInt();
		}

		for (int i = 1; i <= n; i++) {
			for (int j = 0; j <= v; j++) {
				if (j >= vol[i - 1])
					dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - vol[i - 1]] + vol[i - 1]);
				else
					dp[i][j] = dp[i - 1][j];
			}
		}
		System.out.print(v - dp[n][v]);
	}
}

思路：

• 感觉为动态问题，但其问的是最小剩余空间，转换为能够用到的最大空间，即与01背包问题类似；

• 状态转换方程：如上代码循环部分所示；

  dp[i][j]:处理了前i个物品后，背包容量为j的情况下，能够使用的最大空间；

---